 |
Special Positions |
 |
Special Positions |
Special Positions
The space-group diagram of Pnma on the previous page showed the symmetry-equivalent positions for an atom (or ion or molecule) sited on a general position, x,y,z, within the unit cell. In the crystal structures of organic and organometallic compounds, it is very common for the molecules to occupy general positions within the unit cell unless the molecule possesses a point-group symmetry which can coexist with some of the point-group symmetry elements of the space group. When atoms are positioned on point-group symmetry elements of a space group, they are said to be on special positions. This is illustrated below using the crystal structure of SF6 as shown earlier, but with the symmetry elements of the space group C2/m now shown superimposed upon the figure:
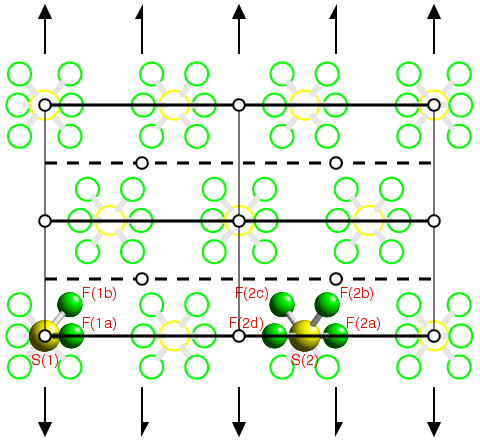
You now get the answer to the question raised in the introduction. From the figure, it can be seen that the sulphur hexafluoride molecules all lie on the mirror planes in this space group. However, one-third of the molecules (labelled S(1)) also lie on a point of inversion, whereas two-thirds do not. Those molecules with mirror symmetry and inversion symmetry also have a twofold rotation axis passing through them as shown by the black arrows. Thus the point-group symmetry of the two crystallographically distinct molecules in the crystal is 2/m for S(1) and m for S(2).
It is important to realize that when an atom lies on a special position, the symmetry operators for that space group generate fewer unique positions within the unit cell. In the above example, the fluorine atom labelled F(1b) lies on a general position, i.e. the atom has point symmetry 1, so that the symmetry operators of the space group C2/m generate 7 other symmetry-equivalent atoms within the unit cell. By contrast, for the sulphur atom labelled S(1), the symmetry operators generate only 1 more symmetry-equivalent position. This result is summarised in the table below:
| Atom | Point Symmetry | No. |
|---|---|---|
| S(1) | 2/m | 2 |
| F(1a) | m | 4 |
| F(1b) | 1 | 8 |
| S(2) | m | 4 |
| F(2a) | m | 4 |
| F(2b) | 1 | 8 |
| F(2c) | 1 | 8 |
| F(2d) | m | 4 |
| Total | - | 42 |
This example demonstrates also that there can be more one than one molecule in the so-called asymmetric unit of the unit cell. The concept of an asymmetric unit forms the subject of the next page.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |