Asymmetric Unit

Asymmetric Unit

Course Material Index

Section Index

Asymmetric Unit

The asymmetric unit of a space group is that part of the crystallographic unit cell which can be used to generate the complete unit cell by the symmetry of the space group. Only the coordinates of the atoms in the asymmetric unit are deposited in the various crystallographic databases. The generation of the remainder of the contents of the unit cell is normally a black box operation done by a computer program. The choice of asymmetric unit is not unique as illustrated by the following three diagrams for the monoclinic space group P2₁.

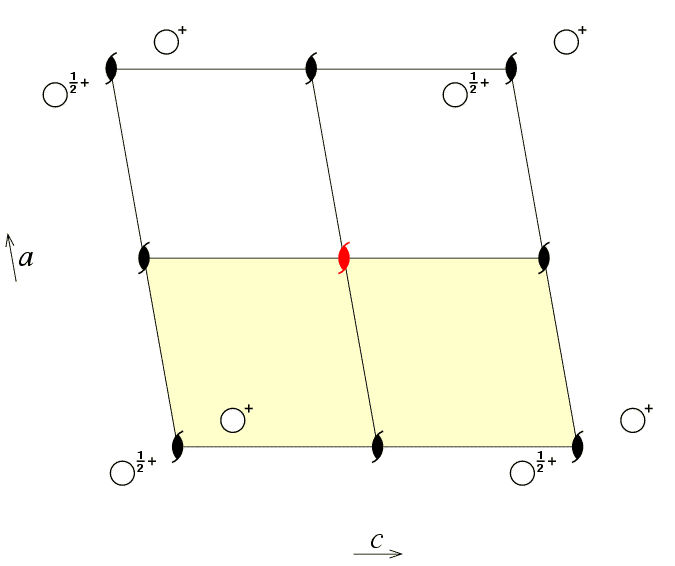
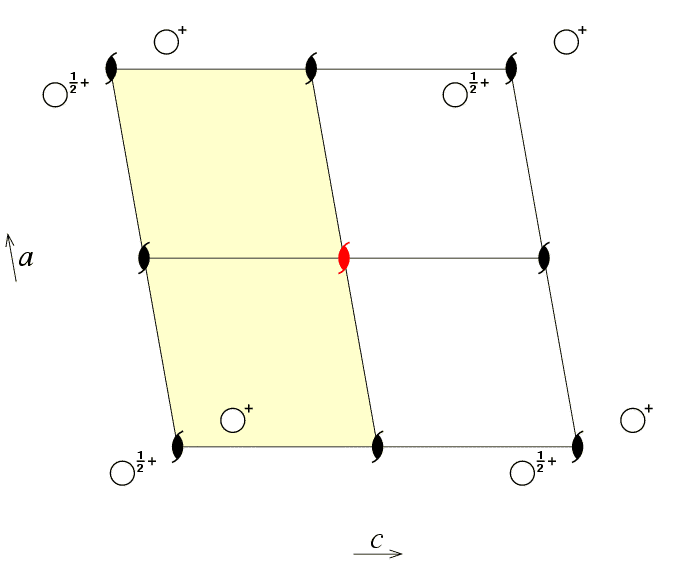
The first figure shows an asymmetric unit (shaded in pale yellow) defined by the coordinate ranges 0 ≤ x < 1/2, 0 ≤ y < 1, 0 ≤ z < 1. Thus the volume of the asymmetric unit is half that of the unit cell in this instance:

The top half of the unit cell (in white) is related to the asymmetric unit (in pale yellow) by the two-one screw axis in the middle of the unit cell (shown in red) with coordinates 1/2,y,1/2.

The next figure shows an alternative choice of asymmetric unit for the same space group, but this time with the asymmetric unit defined by the coordinate ranges 0 ≤ x < 1, 0 ≤ y < 1, 0 ≤ z < 1/2:

Notice that as with the first figure, the open circle shown with height 1/2+z is in the other half of the unit cell to the asymmetric unit containing the open circle at height +z. Both these choices of asymmetric unit have the same range for the y coordinate, and the same symmetry operator relates the two halves of the unit cell.

Can one choose an asymmetric unit with a different range for y? The third figure of space group P2₁ viewed down the c axis shows just such a possibility for the asymmetric unit.

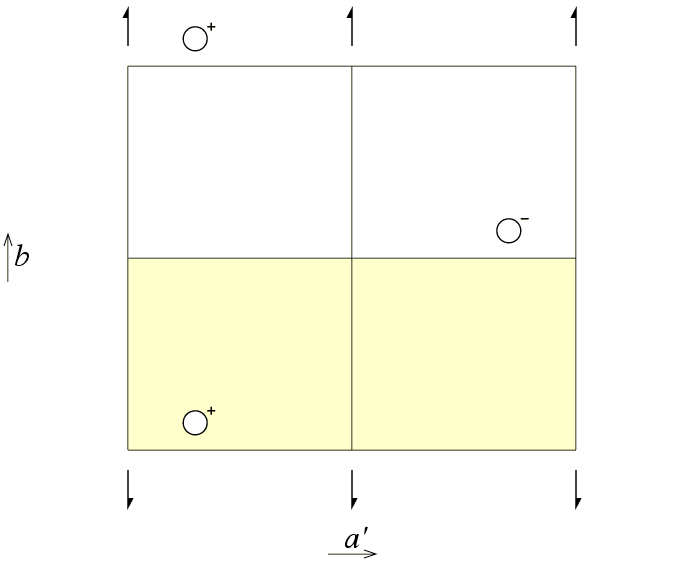
The asymmetric unit is now defined by the coordinate ranges 0 ≤ x < 1, 0 ≤ y < 1/2, 0 ≤ z < 1. Again, it is the same screw axis at the centre of the unit cell with coordinates 1/2,y,1/2 that relates the asymmetric unit (in pale yellow) with the other half of the unit cell (shown in white).

These figures illustrate that the choice of the asymmetric unit is something fixed by the crystallographer and that it is choice is not an intrinsic property of the crystal. Fourier programs that calculate electron density maps make use of asymmetric units with straight edges as shown in the three previous illustrations. However, the asymmetric unit is not required to have nice straight lines as shown in the figures! In fact, crystallographers frequently choose asymmetric units that are determined by the "outline of the molecule", which is all but linear. This is shown schematically in the figure below for the organic molecule S(-)-α-bromobenzylmethylsulfone [1], illustrated using coordinates extracted from the Cambridge Structural Database:

This example was chosen due to its relatively short b axis, which allows a pseudo two-dimensional asymmetric unit to be picked out as shown in purple. In this example, there are two molecules in the unit cell, which are symmetry related by the two-one screw axis shown in red. More precisely, it is the centre of gravity of the two molecules that lies within the unit cell, since a few atoms lie outside it.

It is usually more convenient to describe a crystal structure in terms of atomic coordinates of atoms that belong to a single complete molecule; by doing this the crystallographer is implicitly considering an asymmetric unit of the type outline in purple above and which extends just beyond the limits of the unit cell. Note that although both methyl (-CH₃) groups are shown outside the unit cell, there will also be two methyl groups (not shown) within the unit cell; the latter belong to two other molecules whose centres of gravity lie outside the unit cell.

You should note that, whatever choice is made for it, the asymmetric unit will always comprise one half of the volume of the unit cell for this particular space group. The number of asymmetric units per unit cell for each space group is determined by the lattice centring (i.e. P, A, B, C, F, I, or R) and the crystal class. The concept of crystal class will be discussed next.

[1] Crystal structure by G.D.Andreetti, G.Bocelli, & P.Sgarabotto published in Crystal Structure Communications, (1973), 2, 519.

Course Material Index

Section Index

Author(s): Jeremy Karl Cockcroft