 |
Space-Group Diagrams |
 |
Space-Group Diagrams |
Space-Group Diagrams
Space group diagrams are designed to show the positions of the the symmetry elements of the space group within a single unit cell. In addition, they also show how various parts of the unit cell are symmetry related. Atoms (or molecules) related by symmetry are said to be symmetry-equivalent.
A typical space-group diagram is shown below for the orthorhombic space group with the symbol Pnma:
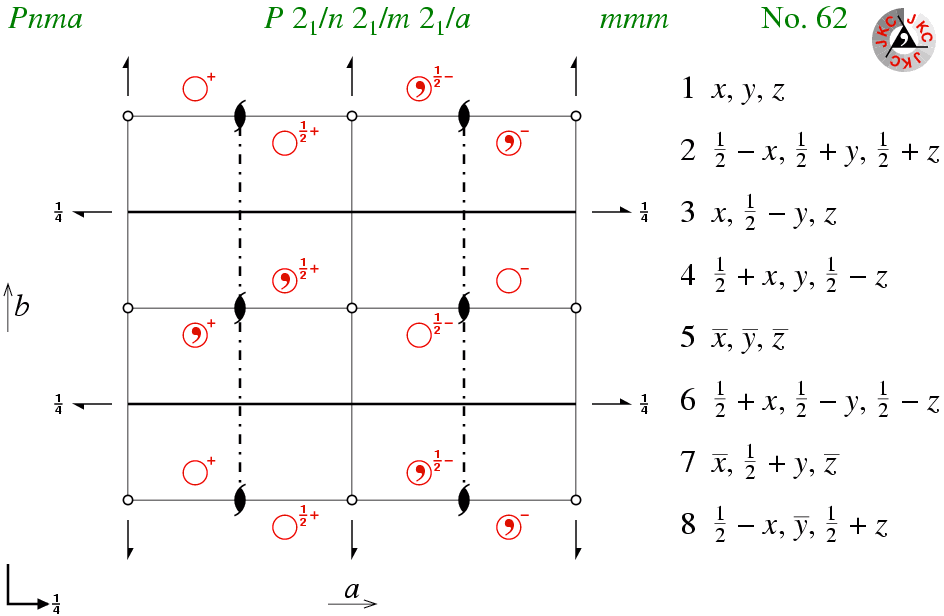
The diagrams with the "JKC" logo in the top right-hand corner are drawn with the origin in the bottom left-hand corner (in contrast to the IUCr International Tables for Crystallography where the origin is taken as the top left-hand corner), and with the third axis perpendicular to, and coming out of, the plane of the screen. The three axes a, b, c form a right-handed system; axes projected on to the plane of the screen are labelled accordingly.
![]() Space group diagrams like the one shown above correspond to
the flat projection
discussed in the previous symmetry section.
The diagrams show the position of all symmetry elements
within (or on the edge of)
the unit cell.
Can you identify the symmetry elements shown in this diagram? (You may
need to refer back to the table
given in an earlier section.)
Space group diagrams like the one shown above correspond to
the flat projection
discussed in the previous symmetry section.
The diagrams show the position of all symmetry elements
within (or on the edge of)
the unit cell.
Can you identify the symmetry elements shown in this diagram? (You may
need to refer back to the table
given in an earlier section.)
The position of an arbitrary point in the unit cell, usually chosen to be near the origin in the space-group diagram, is shown using an open circle, as for the point-group diagrams. For space group Pnma, there are eight symmetry equivalent positions within the unit cell; the associated symmetry operators are listed adjacent to the diagram as x,y,z, etc. In order to be able to make estimates of the positions of symmetry equivalent positions within the unit cell, the latter has been divided up into four quadrants (by thin black lines). Thus the whole diagram represents one unit cell (and not four!).
It is important to realize that the number of symmetry operators for a space group is actually infinite since space groups are non-finite groups due to the presence of the primitive lattice translations: these translations, which are common to all 230 space groups, are sometimes written in symbolic form as t(1,0,0); t(0,1,0); and t(0,0,1). The infinite set of symmetry operators can be reduced to a finite (and hence managable) group by removing the the integer part of any translational component of the symmetry operator. For the case of space group Pnma, this reduces an infinite number of symmetry operators to just eight unique ones, as listed above.
The diagrams show also the unique space group number associated with each space group. In addition, short and full space group symbols are given above each diagram; for space group 62 the short symbol Pnma gives only the lattice centring plus the mirror and glide planes, while the full symbol emphasises the presence of the two-one screw axes as well. Finally, above each diagram is the point-group symbol for the crystal class (see later page). For the space group Pnma, the crystal class is mmm.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |