Introduction to Space Groups

Introduction to Space Groups

Introduction

In order to describe fully the crystal structure of a particular substance, a knowledge of the contents of the unit cell is required. The translational symmetry of the lattice then repeats this information ad infinitum throughout the crystal. However, the unit cell may also contain additional symmetry elements, other than simple lattice translations, such as rotation or screw axes. Under these circumstances, it is not necessary to describe the whole unit cell, but only one part of it. The additional symmetry elements within the unit cell then determine the remainder of its contents. This is illustrated by the following figure showing a single unit cell of the substance sulphur hexafluoride, SF₆, at low temperature:

In this example the unit cell contains 6 molecules of SF₆; an atom (or molecule) is considered to be inside the unit cell as long as its fractional coordinates are all in the range 0 ≤ x,y,z < 1. If the contents of the unit cell were to be described without the use of symmetry, then a total of 42 (6 × 7) coordinates would be required. If the symmetry of the unit cell is known, then the crystallographer needs to specify only the atomic coordinates of the 8 shaded atoms in the above figure; the coordinates of the other 34 within the unit cell can all be generated given the symmetry of the crystal. Thus symmetry can be used to shorten considerably the description of a crystal structure; more importantly, a knowledge of the crystal symmetry reduces the number of atomic coordinates that have to be found in the determination of a crystal structure.

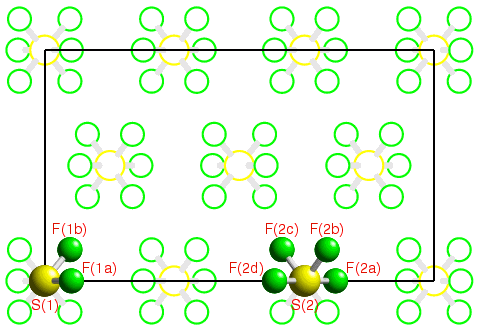
Space-group symmetry is a combination of the translational symmetry of a lattice together with other symmetry elements such as rotation and/or screw axes. The determination of space-group symmetry of material is an essential step in structure analysis since it minimises the amount of information needed for the complete description of the contents of the unit cell. By describing a few of the most commonly-observed space groups in detail, this section on space-group symmetry attempts to cover most of the pertinent concepts of space-group symmetry required in this course.

In the previous section on point-group symmetry used, the symmetry of an isolated molecule of sulphur hexafluoride was given as m-3m. In this example, there are two such molecules in the unit cell, neither of which has symmetry m-3m due to the presence of neighbouring molecules within the crystal. Which one of the two molecules labelled S(1) or S(2) do you think has the highest point-group symmetry in the crystal structure, and why? (You will get the answer in the next few pages, but try to work out the answer before reading on.)

Course Material Index

Section Index

Author(s): Jeremy Karl Cockcroft