 |
Point-Group Diagrams |
 |
Point-Group Diagrams |
![]() The majority of the table is reference material.
The majority of the table is reference material.
Point-Group Diagrams
The previous two pages were an introduction to the concepts of molecular point symmetry and the crystallographic notation used to define it. We now return to the concept of stereographic projections to illustrate the symmetry elements of the 32 crystallographic point groups.
The figure below shows a ball & stick figure of a water molecule viewed down the twofold rotation axis that passes through the central oxygen atom. As pointed out earlier, this molecule has the crystallographic point-group symmetry mm2. Superimposed on the molecule is the steroegraphic diagram for this particular point group.
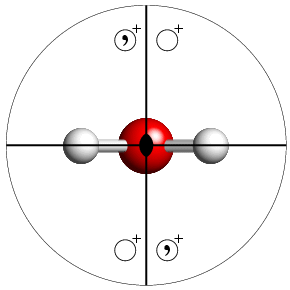
The table that follows contains clickable links to stereographic diagrams for all of the 32 crystallographic point groups. Note that additional comments are made only concerning the figures of the low-symmetry point groups.
| Crystal System | 32 Crystallographic Point Groups | ||||||
|---|---|---|---|---|---|---|---|
| Triclinic | 1 | -1 | |||||
| Monoclinic | 2 | m | 2/m | ||||
| Orthorhombic | 222 | mm2 | mmm | ||||
| Tetragonal | 4 | -4 | 4/m | 422 | 4mm | -42m | 4/mmm |
| Trigonal | 3 | -3 | 32 | 3m | -3m | ||
| Hexagonal | 6 | -6 | 6/m | 622 | 6mm | -62m | 6/mmm |
| Cubic | 23 | m-3 | 432 | -43m | m-3m | ||
Special Positions
The above figure also introduces the concept of special positions. This is a term frequently used to describe the coordinates of atoms in a crystal structure that do not have the general coordinates, x,y,z. In the above figure, the hydrogen atoms lie on one of the mirror plane and the oxygen lies on the twofold rotation axis formed by the intersection of the two mirror planes. Applying the various symmetry elements to one of the hydrogen atoms can generate the second, but no more. Likewise, applying the symmetry elements to the oxygen atom generates only the original atom and nothing else. Thus all three atoms lie on so-called special positions, and only the coordinates of two of them are required in order to completely specify the position of the water molecule given its point-group symmetry of mm2. This concept will be developed further in the later section on space-group symmetry.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |