Diffraction Symmetry

Course Material Index  Section Index  Previous Page  Next Page 

Diffraction Symmetry

There are two fundamental reasons for learning about point-group symmetry in crystallography. The first is so that the symmetry of atoms and molecules in a crystal structure can be understood. The second is so that the point-group symmetry of the data can be interpreted since this provides part of the information that leads to the determination of the space-group symmetry of the crystal.

The diffraction experiment measures the spacing of the spots from which the reciprocal lattice is derived. The page on crystal systems listed the constraints on the real-space unit-cell parameters for the various crystal systems. There are similar constraints that apply equally-well to the reciprocal-space unit-cell parameters, which are listed in the table below:

Note: The trigonal unit-cell parameters given here are for the case of rhombohedral cell axes with a rhombohedral lattice. For the primitive trigonal unit cells, the parameters and constraints are identical to those of the hexagonal crystal system.

Note the similarity in the constraints between real and reciprocal unit cell lengths: lengths that are equal in real space of the crystal will show a corresponding constraint in the diffraction data. Likewise unit cell angles that are 90° in the crystal will exhibit 90° angles in reciprocal space.

In the monoclinic crystal system two of the angles are constrained to be 90° in both real and reciprocal space. The remaining angle is also constrained such that β + β* = 180°. This is shown in the above figure where the directions of the real-space vectors are shown in purple and those of reciprocal-space are shown in red. You should be able to see that the a* is perpendicular to c and that c* is perpendicular to a. b and b* are colinear and perpendicular to the plane of the screen. In the hexagonal system there is a similar constraint such that γ + γ* = 180°; given that γ is 120°, this implies that γ* is 60° for this crystal system.

In addition, the diffraction experiment measures the intensity of the reciprocal-lattice points, which are proportional to the square of the structure factors, F(hkl). Friedel's law states that, in the absence of anomalous dispersion effects, |F(hkl)| = |F(-h-k-l)|. By virtue of this law the reciprocal lattice weighted with |F| always contains a point of inversion in the absence of anomalous dispersion, even when this symmetry element is not present in the crystal structure. Thus the point-group symmetry of the reciprocal lattice is centrosymmetric.

In a single crystal experiment, it is normally possible to measure the intensity of the individual reflections, I(hkl), and to display them as diffraction spots of various sizes, spaced out in a reciprocal lattice, as illustrated in the (clickable) figure below:

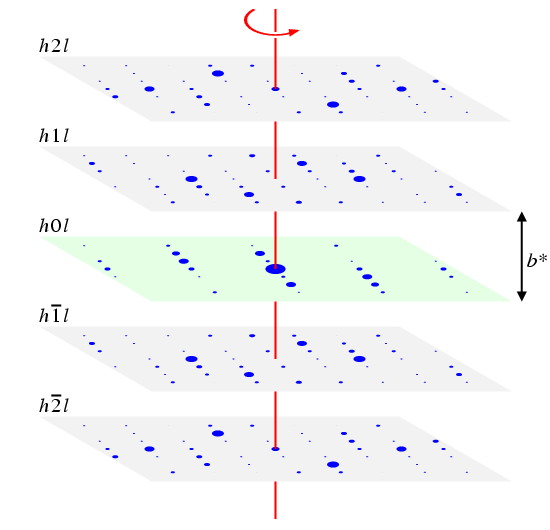
The above figure shows generated single-crystal "data" for a crystal with monoclinic symmetry. Each of the hkl (clickable) planes in the above figure exhibits twofold rotation symmetry, shown by the red line. Thus the symmetry of the spots with indices hkl is the same as those with indices -hk-l. There is also mirror symmetry perpendicular to the twofold rotation axis, shown as a green plane, which relates I(hkl) to I(h-k,l). Due to Friedel's Law, the intensity data are also centrosymmetric. Therefore, the point symmetry of the data is 2/m, which is a monoclinic point group. Notice that the point group can only be determined by examination of the whole data set and not just a single plane.

Finally, you may notice that the zone plane h0l (so-called because k = 0) is different to the others. The additional symmetry revealed by the "missing" spots in this plane will be discussed in a later section of the course material.

Laue Classes

The eleven centrosymmetric point groups which describe 3-dimensional diffraction symmetry are known as the Laue classes (often still referred to as Laue groups). They are listed in the table below:

From the table it can be seen that for the low-symmetry crystal systems there is a single corresponding symmetry for the diffraction data, but that for the high-symmetry crystal systems, two possibilities exist. The implications of this will not be discussed here.

Powder Diffraction

Powder diffraction experiments measure only 1-dimensional data, i.e. they measure intensity as a function of d spacing only. It is therefore not possible to determine the Laue class directly from the data. One effect of this will be discussed in detail in a later section of the course material concerning space-group determination.

However, compared to single-crystal diffractometers, the higher 2θ resolution of most powder diffractometers makes them more sensitive to the determination of lattice geometry. This provides some compensation for the loss discussed above. Another aspect of measuring 1-dimensional data is the superposition of symmetry-equivalent reflections: the subject of reflection multiplicity forms the subject of the next page.

Course Material Index  Section Index  Previous Page  Next Page