Logo Molecular Point Symmetry
Course Material Index  Section Index  Previous Page  Next Page 

Molecular Point Symmetry

Isolated molecules provide many examples of crystallographic (and non-crystallographic) point-group symmetry. Before providing a formal table of the 32 crystallographic point groups, it is instructive to see how the rotation and rotary-inversion axes interact in some molecular structures.

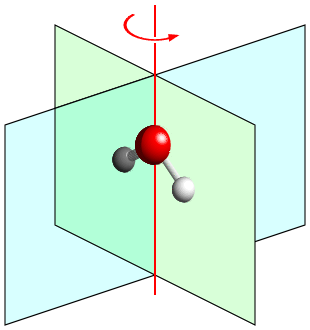
The diagram below shows a single water molecule. The molecule is planar so that the three atoms (O and two H) all lie in the mirror plane shown in green. In addition, there is a second mirror plane, shown in blue, that is perpendicular to the first mirror plane: the two hydrogen atoms are symmetry related by this symmetry element, which passes through the central oxygen atom. Finally, the combination of the two mirror planes automatically implies the presence of a twofold rotation axis, shown in red, that passes through the oxygen atom and along the line of intersection of the two mirror planes. As with all point groups, there is also the identity operation, 1. The combination of symmetry elements 1, 2, m, and m′ forms the crystallographic point group with the symbol "mm2".

H2O

The following table provides examples of molecules with different point-group symmetries. The classification of low to high symmetry is based on both the number and order of the symmetry axes present. In each case, you should be able to see different ways in which the symmetry elements 1, 2, 3, 4, 6, -1, m, -3, -4, and -6 can be combined. The table is not exhaustive, illustrating only 21 of the 32 crystallographic point groups.

SymmetryExamples
Low

High

 CH3CH(NH3)CO2, CHFCl-CHFCl,
CHFBr-CHFBr, HOCl, CHBr=CHBr
C9H12Cl4, CHCl=CHCl, C2O4=
CH2=C=CH2, SbCl5=, Pt(CN)4=
Cr(C2O4)3−, CH3CCl3, C6H12
B(OH)3, C6(CH3)6, CO3=, C6H6
Co(NO2)6−, SO4=, SF6

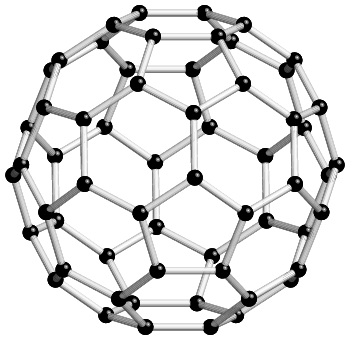
It is important to realize that many molecules and ions may not have a crystallographic point-group symmetry, e.g. linear molecules or ions, and S8. A topical example is provided by the C60 molecule, shown below, which is based on carbon atoms in perfect pentagonal and hexagonal rings. Isolated molecules have fivefold rotation axes passing through the centre of each pentagonal ring, together with threefold rotation axes passing through the middle of each hexagonal ring. The symmetry of the molecule is described as icosahedral.

C60

It is important to realize that the point symmetry of ions and molecules are usually lower in a crystal structure than in the gaseous (or liquid) state. Simple anions such as oxide, O2-, are spherical when considered in vacuo, but their symmetry is reduced when the impact of the surrounding atoms is taken into account. This will be discussed in more detail under space group symmetry.

Course Material Index  Section Index  Previous Page  Next Page 
© Copyright 1995-2006.  Birkbeck College, University of London. Author(s): Jeremy Karl Cockcroft