Using Rietica: V. Crystallographic Model

Course Material Index  Section Index  Previous Page  Next Page 

Crystallographic Model

Once the background has been defined, you can now set-up the crystallographic model: all of the options required will be found in the Model pull-down menu:

Starting with the General option, the first item to set is a title for the crystal structure being refined:

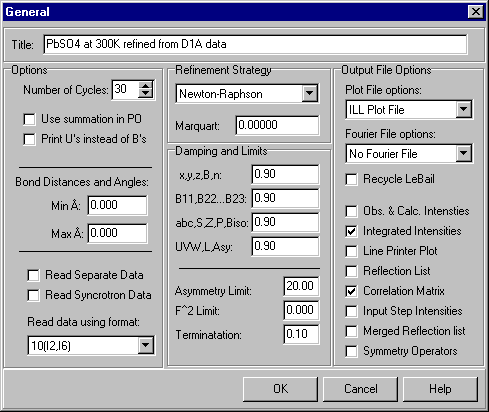
There should be no need to set any other parameters at this stage, though it will be useful to reset the parameters that determine the calculation of bond lengths and angles later.

The main menu for the crystal structure parameters is Phases:

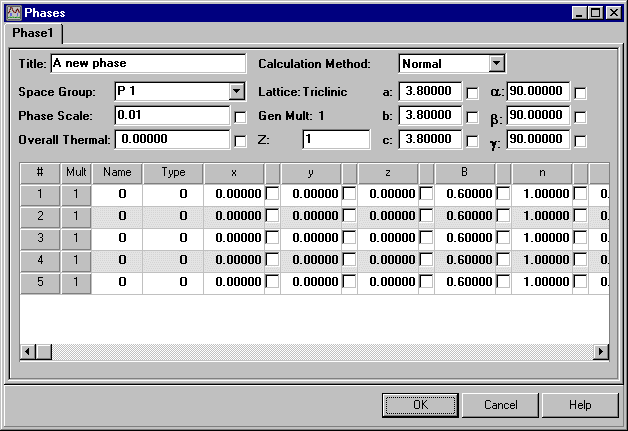
The program can handle multiple phases, so the title here refers to the particular phases being defined: the lead sulphate example used here is single phase. Then set the space group. Although there is a pull-down menu of standard space-group symbols, you can type in the space group symbol direct, which is useful for the non-standard settings. (Note the spaces between the different symmetry components in the space group symbol.) The lattice parameters a, b, and c need to have their values initialised (as given in the case study).

You can then start inputting the coordinates. Enter an atom name and then its Type: the Type option should match the chemical element name so that the correct scattering factor is used (via a lookup table). This is followed by the fractional coordinates of the atom x, y, z (as given in the case study), an isotropic thermal displacement factor B (which can take the default value 0.6 Å²), and a site occupancy value n.

Rietica uses the traditional crystallographic definition of n: number of atoms per unit cell divided by the number of symmetry equivalent general positions (which is 8 for Pbnm). For an atom on a special position, this number will be less than unity. In addition, if the site is not fully occupied, the number will be less than unity too. Other programs may use a different definition: for example, n may be defined as the number of atoms per unit cell, or it may be defined as being equal to unity when the site is fully occupied, irrespective of whether the atom lies on a special position or not. In this case, Pb, S, O(1), and O(2) all lie on a mirror plane (though not all on the same one), and so the value of n must be set to one-half. Leave the values of B11, B22, etc. as zero, since these are only used to describe atoms with anisotropic temperature factors.

Finally, click the box after the value of the phase scale factor to indicate that this value is to be refined. A tick character will appear:

You will notice an empty box after each refinable parameter: when the box is blank, the parameter is fixed, i.e. not refined during the least-squares minimisation process; when the box is ticked, the parameter is refined. Note that the value of the parameter will not be updated unless you have clicked on Finish after n cycles (Step) of refinement (as described on the next page).

At this point, you do not need to revisit the Histograms or Sample options (though there is no harm in viewing their contents), and so you are now ready to begin...

Course Material Index  Section Index  Previous Page  Next Page