 |
Case Study |
 |
Case Study |
Case Study
A case study is now given, to provide a practical demonstration of the Rietveld method using "round-robin" data obtained on lead sulphate on a warm day (300 K) in 1989 using the powder neutron diffractometer D1A at the ILL, Grenoble. (The data were collected and kindly supplied by Dr. Alan Hewat.) One of the objectives of the exercise was to test various versions of the Rietveld program, and how they were being applied. Starting with the following information, we shall see how the refinement might have taken place in practice.
At room temperature, the crystal structure of lead sulphate has space-group symmetry Pbnm (which is a non-standard setting of no. 62 Pnma). The symmetry operators for this setting are given in the table below. In practice, virtually all Rietveld program codes do not require the centrosymmetrically-related symmetry operators in the right-hand side of the table, but do check the manual for the version of the Rietveld program that you happen to use.
| Space group 62 : Pbnm | |||||||
|---|---|---|---|---|---|---|---|
| x, | y, | z | 1 | -x, | -y, | -z | -1 at (0,0,0) |
| 1/2-x, | 1/2+y, | z | b at (1/4,y,z) | 1/2+x, | 1/2-y, | -z | 21 at (x,1/4,0) |
| 1/2+x, | 1/2-y, | 1/2+z | n at (x,1/4,z) | 1/2-x, | 1/2+y, | 1/2-z | 21 at (1/4,y,1/4) |
| x, | y, | 1/2-z | m at (x,y,1/4) | -x, | -y, | 1/2+z | 21 at (0,0,z) |
Intial values for the unit-cell parameters are given below. It would normally be better to start with slightly more precise values (e.g. 2 decimal places), though in this instance this is not a problem. This is particularly true if the structure being refined is of lower symmetry than orthorhombic and/or the cell metric tensor is close to that of a higher-symmetry crystal system.
Cell parameters : a = 7.0 Å, b = 8.5 Å, c = 5.4 Å
Approximate coordinates for the structure of PbSO4 are given in the table below:
| Atom | x | y | z | N |
|---|---|---|---|---|
| Pb | 0.15 | 0.20 | 1/4 | 4 |
| S | 0.20 | 0.50 | 3/4 | 4 |
| O(1) | 0.10 | 0.60 | 3/4 | 4 |
| O(2) | 0.00 | 0.30 | 3/4 | 4 |
| O(3) | 0.30 | 0.40 | 0.9 | 8 |
The starting coordinates are rather crude: calculation of the sulphate ion
geometry using these coordinates give values of 1.1 to 2.2 Å
for the S-O bond lengths and 73° to 114° for the
![]() O-S-O bond angles;
these are someway off those expected for an ideal tetrahedron!
You will see that four of the crystallographic atoms lie on a special position
in this space group, namely on the mirror plane. The number of "molecular
units", Z, per unit cell is 4 for lead sulphate: hence the site
occupation number, N, is 4 for Pb, 4 for S, and a total of 16
for the three oxygen positions, O(1), O(2), and O(3).
O-S-O bond angles;
these are someway off those expected for an ideal tetrahedron!
You will see that four of the crystallographic atoms lie on a special position
in this space group, namely on the mirror plane. The number of "molecular
units", Z, per unit cell is 4 for lead sulphate: hence the site
occupation number, N, is 4 for Pb, 4 for S, and a total of 16
for the three oxygen positions, O(1), O(2), and O(3).
The isotropic temperature factor (more correctly called an atomic-displacement parameter) for each crystallographic atom type was initialised to a typical value: in this instance the starting value for Biso was chosen to be 1.0 Å2.
The nominal wavelength was as listed below. In addition, the resolution function of the diffractometer is characterised by the UVW values given below. It is important to know all of the instrumental characteristics before starting any Rietveld refinement: these can usually be obtained by collecting data on a standard sample such as silicon powder and fitting the instrumental parameters (by the Rietveld method) to the diffraction pattern. The peak-shape function for D1A is better than 95% Gaussian, though with noticeable asymmetry below 30° 2θ.
Instrumental : λ = 1.909 Å, U = 0.2°2, V = -0.5°2, W = 0.5°2
For the particular refinement given here, the background count of the diffraction data was estimated graphically as shown in Figure 1. A refinable background function could have been used, but it is open to debate whether it would have given much better results in this instance. At this point the weighted-profile R-factor is 100% since there is no structural model to contribute diffraction intensity to the calculated profile.
The first step in any Rietveld refinement procedure is to refine the overall scale factor, c. Its initial value is arbitrarily set to 1.0 and it should only require 1 cycle of least squares to refine its value: the reason is that the scale factor is the only "linear" parameter in the least-squares procedure; all the other parameters are non-linear. At this point, the R-factor dropped to only 81% with the fit shown in Figure 2. An expanded region of Figure 2, is shown in Figure 2a. It is very important to look at the profile plots at these early stages of refinement since a quick look now may save an enormous amount of wasted time on refinements that will never converge correctly. For example, common errors that are easily spotted at this stage include mistyped wavelengths, lattice parameters, zero error, and other instrumental parameters. It is important that the positions of the calculated peaks approximately match those of the observed peaks, at least for the large d spacings (i.e. the low-angle part of the diffraction pattern in this instance). A good match to the intensities is less critical at this stage. At this point, the expected R-factor of 3.5% indicates that the data is of high statistical quality. Note that the observed profile appears "higher" than the calculated profile: this is quite normal and is a consequence of the weighted least-squares procedure.
The observed, calculated, and difference profile plots can often be used to indicate the next step in the refinement. The expanded region of Figure 2, shown in Figure 2a, clearly shows a slight mismatch in observed and calculated peak positions indicating that refinement of the unit-cell parameters and/or any peak-displacement parameters, such as a 2θ zero error, should be the next step in this refinement. This should always be next step when the unit cell is not known precisely; by contrast, if the lattice parameters are known very precisely for the particular conditions of the data collection, then refinement of these variables at this stage can actually make the parameters go astray! Likewise, if the 2θ zero error is known to be zero, then it may be better to leave it fixed at this value until much later in the refinement procedure, especially on those occasions when refinement of the lattice parameters is problematic.
In this instance, both unit-cell parameters and 2θ zero error were refined. After 6 cycles of refinement, the weighted-profile R-factor reduced to 61%, and the profile fit shown in Figure 3 was obtained. The expanded section shown in Figure 3a demonstrates the improvement in the match between observed and calculated peaks positions. You should also be able to see an improvement in the match in the high-angle region of the pattern for the group of peaks at around 145°. The additional variables refined to the following values:
Unit-cell parameters : a = 6.950(1) Å, b = 8.465(1) Å, c = 5.386(1) Å, and 2θzero = -0.14(1)°
Note that the scale factor is still being refined at the same time as the lattice parameters and zero error: previously refined values should not normally be fixed when new parameters are added to the least-squares procedure. The estimated standard deviations (esd's) on the refined unit-cell parameters are relatively high at this point due to the fact that the fit is still far from satisfactory. The lattice parameters are amongst the most non-linear parameters in the least-squares procedure; consequently it may take more cycles of refinement than normal for the procedure to converge. This is especially true when the initial values differ significantly from the true values; in extreme cases convergence to a false minimum is a serious possibility.
Once a good match has been obtained between observed and calculated peak positions, attempts can be made to improve the match in peak intensities. The key parameters here are going to be the atomic coordinates since refinement of these will affect the relative intensities of neighbouring peaks in the diffraction profile. At this stage, strategies vary depending on the whether the data have been obtained from an X-ray or neutron diffractometer. The usual approach will be to vary the atomic coordinates of the strongest scatters with the most degrees of freedom, i.e. refine atoms on general xyz positions first in preference to atoms on special positions, e.g. those with coordinates (x,y,3/4) in this case study. Refinement of the O(3) atomic coordinates reduced the weighted-profile R-factor from 61% to 42.4% and produced the fit shown in Figure 4.
The atomic coordinates of O(3) refined to the following values:
O(3) atomic coordinates : x = 0.306(1), y = 0.423(1), z = 0.966(1).
It is generally better to increase the number of refined parameters progressively, so the next step involved refinement of the atomic coordinates of Pb, and then O(1) and O(2). Note that for neutrons, sulphur is the weakest scatterer, in marked contrast to the X-ray case. The weighted-profile R-factor dropped first to 38.7% (after refinement of the atomic coordinates of Pb) and then to 29.4% (following further refinement of the atomic coordinates of O(1) and O(2)). The fit at this stage is shown in Figure 5.
In general, it is better to refine the atomic coordinates of weak scatterers after those of strong ones. In this context, it is worthwhile keeping in mind that atoms with large atomic-displacement parameters may effectively be weaker scatters than those with small ones. Refinement of the two free atomic coordinates of sulphur led to a surprisingly large improvement in the fit as shown in Figure 6. Rwp was now 12.2%.
Despite the relative weak scattering of the sulphur atom, a big improvement is observed for the fit. You may wonder why; it is tempting to argue that this is due to the the fact that the starting coordinates of the sulphur atom were particularly poor: compare the currently refined values below to those used initially.
S Atomic Coordinates : x = 0.1834(9), y = 0.4338(7), z = 3/4.
However, if the order of refinement were O(3), S, Pb, O(1), and finally O(2), then the most noticeable drop in R-factor would be in the last step: it only requires one atom to be significantly out in terms of its atomic coordinates for the R-factor to remain high.
When the R-factor is this low, visualisation of the difference
profile starts to become more useful than looking at the observed and calculated
profiles alone; in fact the superposition of the calculated on the observed
makes the plot of the observed profile almost redundant at this point.
The esd's on the lattice parameters have now been reduced to between
0.0001 and 0.0002 Å, while those on the atomic coordinates
are in the range 0.0002 to 0.0009. More importantly, the geometry of the
sulphate ion is starting to become chemically reasonable: the S-O distances
now vary from 1.46 to 1.48 and the
![]() O-S-O
angles (108° to 113°) are closer to the ideal tetrahedral value of
109.5°.
O-S-O
angles (108° to 113°) are closer to the ideal tetrahedral value of
109.5°.
You may be tempted to either (a) stop at this point thinking that the fit is not too bad, i.e. quite good, or (b) to add every remaining variable into the refinement process without much further ado. To get the most of out of a data set, it is as important not to over refine the model as to under refine it. The difference fit shown in Figure 6 shows that the overall temperature factor is too small. The calculated peak widths as determined by the resolution-function parameters UVW are quite good, but should also be refined at this point: they take into account a sample-dependant contribution to the peak widths that varies from one sample to the next. Refinement of an overall temperature factor and the values of UVW now reduced the weighted-profile R-factor to 9.5%. The corresponding R-factor based on peak intensities alone is 6.0% and the fit is shown in Figure 7. The most useful part of the plot is now the difference profile, which still shows significant differences between the observed profile and that calculated from the refined model.
The next step depends largely on the type and quality of the data. A powder neutron diffraction data set usually lends itself to the refinement of individual isotropic temperature factors, which may be refined anisotropically for data of high quality. Refinement of individual isotropic atomic-displacement parameters led to the following values:
Temperature Factors, Biso, in Å2 : Pb = 1.6(3), S = 0.7(7), O(1) = 2.2(5), O(2) = 1.7(5), O(3) = 1.6(3)
R-factors : Rwp = 8.9%, Rexp = 3.3%, RI = 5.1%
The relative high values for the oxygen atoms and the lower value for the sulphur atom is indicative of librational motion of the sulphate ion: this type of motion results in greater atomic displacements perpendicular to the S-O bond than along it. In addition, the lead atom is probably being buffeted by the motion of the sulphate group, which may also cause its atomic displacement to be anisotropic. Anisotropic temperature factors, βij, were then refined giving:
R-factors : Rwp = 7.1%, Rexp = 3.3%, RI = 2.8%
The weighted-profile R-factor has dropped slightly, but the intensity R-factor has nearly halved in value indicating that the extra parameters led to a significant improvement in the model structure. Analysis of the thermal ellipsoids showed that the sulphur atom was not anisotropic within experimental error, so this atom was constrained to have an isotropic temperature factor only. Note that the anisotropic temperature factors for atoms on special positions also have symmetry constraints on their component values: the effect of these constraints is evident in the final table given at the end of this page. It is important that critical thinking is employed at this point, not just a quick check on the R values; do not be tempted to vary every parameter under the sun that the particular Rietveld code you are using has to offer!
Other parameters that may be refined at this point are, for example, peak asymmetry parameter(s). In this instance only a slight improvement is to be expected since there are no intense diffraction peaks below 30° for this data set. With the weighted-profile R-factor now at 6.3%, many would be tempted to pack up and go home! The best fit that this author achieved had the R-values given in the final table below with the introduction of just one more parameter, namely η. This accounted for the fact that the peak-shape function is not purely Gaussian in this instance due to sample broadening effects: the pseudo-Voigt function turns out to be a better choice with the peak-shape parameter refining to 0.26, corresponding to a peak that is 74% Gaussian and 26% Lorentzian in character. The final fit is illustrated in Figure 8, and the refined parameters and esd's are listed in the tables below:
Cell parameters : a = 6.94802(7) Å, b = 8.46618(8) Å, c = 5.38904(6) Å
| Atom | x | y | z | B(iso) |
|---|---|---|---|---|
| Pb | 0.1671(1) | 0.1879(1) | 1/4 | - |
| S | 0.1848(3) | 0.4358(2) | 3/4 | 0.93(4) |
| O(1) | 0.0958(2) | 0.5907(1) | 3/4 | - |
| O(2) | 0.0429(2) | 0.3068(2) | 3/4 | - |
| O(3) | 0.3082(1) | 0.4192(1) | 0.9727(1) | - |
| Atom | B11 | B22 | B33 | B23 | B31 | B12 |
|---|---|---|---|---|---|---|
| Pb | 1.58(4) | 1.19(3) | 2.22(4) | 0 | 0 | 0.20(4) |
| O(1) | 2.11(6) | 1.43(6) | 2.95(7) | 0 | 0 | 0.81(4) |
| O(2) | 1.54(6) | 1.73(6) | 2.24(7) | 0 | 0 | -0.77(5) |
| O(3) | 1.60(4) | 1.77(4) | 1.36(4) | 0.07(3) | -0.40(3) | -0.18(4) |
R-Factors : Rwp = 4.2%, Rexp = 3.3%, RI = 2.8%
Structural Parameters :
| Bonds Lengths | Value | Bonds Angles | Value | |
|---|---|---|---|---|
| S-O(1) | 1.450(2) Å | 112.7(2)° | ||
| S-O(2) | 1.471(3) Å | 109.4(2)° | ||
| S-O(3) | 1.482(2) Å | 109.4(2)° | ||
| S-O(3)′ | 1.482(2) Å | 108.5(1)° | ||
| 108.5(1)° | ||||
| 108.2(2)° |
The chosen example is excellent for teaching purposes in that it converges quite quickly to the correct minimum from relatively poor starting parameters. You are unlikely to fall into a false minimum during the refinement of the structure of lead sulphate with this data set. Do not expect all refinements to be this easy: one is more likely to fall into a false minimum than arrive at the true minimum in many cases, particularly when the data are of insufficient quality for the complexity of the structure being refined. In this instance the total number of independent parameters was only 40. It is therefore important from the outset that appropriate data are collected: don't be tempted to use the Rietveld method on, say, data collected for qualitative analysis.
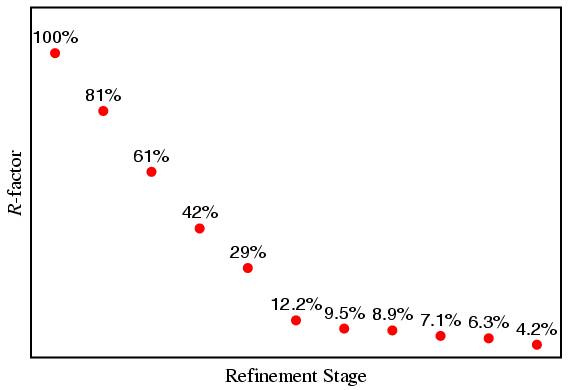
It is instructive to note how the weighted-profile R-factor changed during the different stages of this refinement. This is shown in the plot below, which shows that the R-factor decreased rapidly in the early stages of the refinement, but appeared to change less towards the end of the refinement. However, what is important here is the relative change in this parameter as opposed to an absolute change: the decrease in value from 6.3% to 4.2% in the final stage may be small in magnitude (2.1%), but it is very large in relative terms (33.3%) indicating that the introduction of the extra parameter had a significant effect.
This example is not meant to represent a definitive strategy for the process of structure refinement by the Rietveld method. Far from it! In one sense it does not matter how the best fit is obtained; however, the most accurately-refined values will only be achieved when the best profile fit to the data is obtained with meaningful parameters. In other words, the model has to be correct. A wrong or bad model may produce a fit to the data that some will be tempted to publish: all I can suggest is that you think very carefully about your model structure(s). The Rietveld method is a process of refinement only: it is not a process designed to solve your crystallographic problems, though there may be cases when it can be used to do so. Rietveld programs that claim to "solve" structures ab initio use additional methods within the "standard" code.
| © Copyright 1997-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |