Scattering of X-rays by a Collection of Electrons as in an Atom

Course Material Index  Section Index  Previous Page  Next Page 

Scattering of X-rays by a Collection of Electrons as in an Atom

We must now generalise the previous result to the case of many electrons, not just 2. It is useful to centre our thoughts on an atom as a collection of electrons surrounding a nucleus. Let us imagine a highly conceptual experiment (i.e. one which is virtually impossible to actually perform) in which we hold a single atom still while bombarding it with X-rays and observe the resulting distribution of intensity recorded on a photographic film held behind the atom - see below:

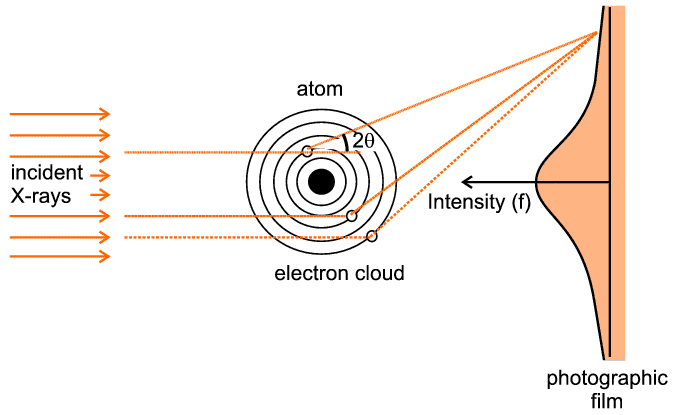
The figure indicates three representative scattering points. There are two significant aspects to this case: first we have to think, in quantum-mechanical terms, of an electron cloud around the atom as a region of charge density probability of finding an electron at any point, rather than thinking of a complete entity such as a single electron. So for example if the representative point is at a (vector) distance r from the centre of the atom and has a local charge density probability of ρ(r), then the chances of finding an electron within a small volume, δV, around this point will be ρ(r)  δV. The second point is that there will be an infinite number of such points if we consider the extent of the whole electron cloud of the atom. The mathematical way of expressing this is to use an integral sign with limits, which signifies that we wish to sum the effect of interest over a range of consideration (such as a complete electron cloud). The final trick, often used in crystallography and diffraction, is to express the scattering as a ratio, in this case the ratio of what scattering we expect from the whole electron cloud compared to what we would have got from a single electron were it to be placed at the centre of the atom ("the origin"): in some ways the situation here effectively becomes a continuous repetition of the previous 2-electron case.

The actual result can be calculated from quantum-mechanical solutions or derived from experimental measurements (though obviously not on a single atom). It is indicated on the photographic film depicted in the above figure: For zero angles (i.e. right behind the atom centre) the scattering is a maximum and equal to the total number of electrons within the electron cloud. As the scattering angle, 2θ, increases there is increasing destructive interference between the X-rays scattered by different parts (e.g. the three points illustrated) of the electron cloud. This gives rise to the very characteristic shape, f, in the above figure. f is often referred to as the atomic scattering factor or form factor; it is so fundamental for diffraction theory that it has been tabulated for most of the atoms and ions in the International Tables for Crystallography (though normally tabulated against sinθ / λ (S/2) rather than against 2θ, and for just one half of the function since the two sides are identical). In the figure below we show the atomic scattering factors, f, for some common atoms:

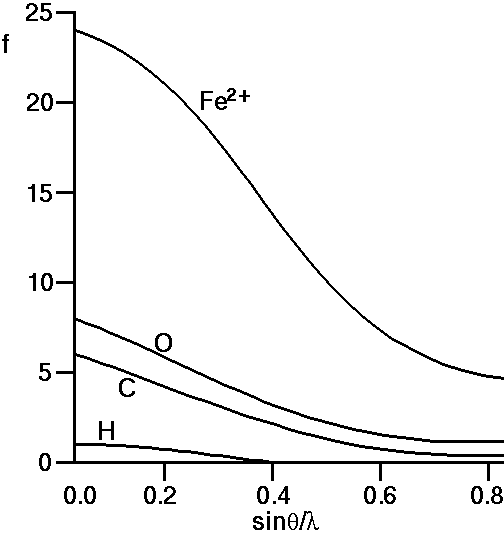
If we look at the f-curve for the oxygen atom we see that it starts ("starts" means sinθ / λ = 0, which also means the scattering angle 2θ = 0) at 8 and decreases thereafter. This means that all 8 of the oxygen's electrons are scattering in phase at zero scattering angle (the maximum point in the above diagram) but as sin&theta / λ (and therefore 2θ) increases the scattering from all 8 electrons becomes progressively out of phase. We can see that this is a plausible result considering the three representative scattering points in the above figure, since they each represent very different associated path lengths as 2θ increases.

Similarly if we observe the curves for carbon and hydrogen we note that their atomic scattering curves start at 6 and 1, respectively the number of electrons for C and H atoms. For iron, Fe, we would expect the curve to start at 26 electrons. However the case shown above is for Fe²⁺ which represents a cationic state of Fe in which it has lost 2 electrons, so indeed f for Fe²⁺ should start at 24.

It is a feature of real systems that the numbers of electrons on different ions tend to congregate together: For example, in aluminosilicate minerals we often find the ionic species: Si⁴⁺, Al³⁺, Ca²⁺, Na⁺, O^2-, which all have 10 electrons. This means that the scattering curves for these 5 ions will all start at 10, and indeed will also be similar thereafter. An important corollary of this is that it will always be difficult to distinguish between these 5 ions on the basis of X-ray diffraction alone; a point well appreciated by mineralogists.

The above discussion assumes that all the electrons scatter as if they were free classical electrons. The scattering power of a bound electron may be more or less than that of a free electron, and its phase may be different as well. Particularly near absorption edges, a phenomenon known as "anomalous scattering" may occur, which modifies the value of f. More information on this effect is described here.

Course Material Index  Section Index  Previous Page  Next Page