 |
Scattering of X-rays by a 1-Dimensional Chain of Atoms or Molecules |
 |
Scattering of X-rays by a 1-Dimensional Chain of Atoms or Molecules |
Scattering of X-rays by a 1-Dimensional Chain of Atoms or Molecules
Moving just slightly closer to reality, we next consider the consequences of X-ray scattering by a chain of atoms or molecules; the situation is idealised in the following diagram (the experiment is again difficult to imagine ever being performed, though perhaps not so impossible as the single electron experiment):
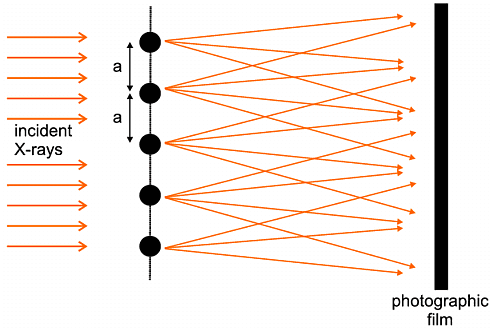
| F(S) = | Σ n |
fne2π i S.rn |
| = | f | e2π i S.r1 + f e2π i S.(r1 + a ) + f e2π i S.(r1 + 2a) + .... |
| I | = f 2 {sin N π a.S / sin π a.S}2 |
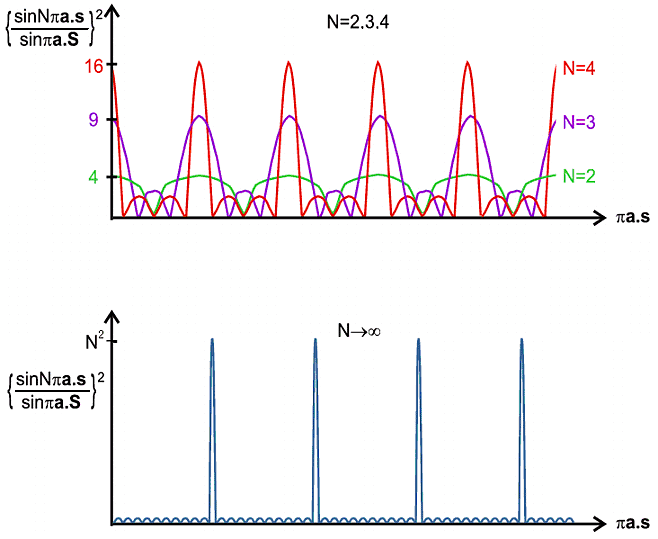
The characteristics of this interference function are very interesting. For small N the pattern is somewhat "lumpy" but as N increases to very high values the repeating peaks become sharper and the background becomes lower and flatter; indeed this function begins to acquire some of the features we would recognise in a diffraction pattern; in fact we only have to multiply this function by f 2 to obtain the intensity (as in the first equation) which is in effect a formula for the diffraction pattern, as illustrated below:
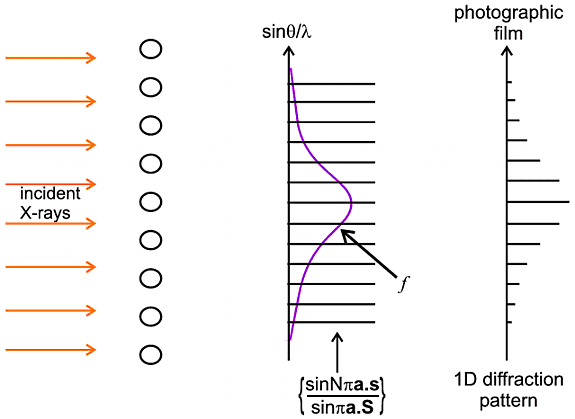
Even though this is a somewhat primitive case, it holds some object lessons for later:
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Paul Barnes Simon Jacques Martin Vickers |