Scattering of X-rays by Two Electrons

Scattering of X-rays by Two Electrons

Course Material Index

Section Index

Scattering of X-rays by Two Electrons

We now consider what happens when, in general, two X-ray photons leave a distant X-ray source at the same moment, are each scattered by an electron, and then meet at a distant X-ray detector. The situation is summarised, again in simplistic terms, by the following schematic diagram.

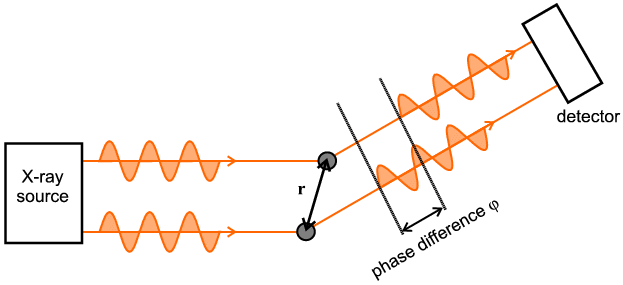Even if two X-rays start off in phase (i.e. at the same time as drawn) the upper X-ray photon will reach the detector before the lower X-ray photon since it has less distance to travel. We would say that the two X-ray photons are out of phase by the time they reach the detector. The phase difference is indicated in the diagram in terms of a length. It is more usual to express this phase difference in terms of an angle (degrees or radians) whereby one angular revolution (i.e. 360 degrees or 2π radians) corresponds to a phase difference of one wavelength; e.g. in the above diagram as drawn, the two waves end up being about one and a quarter wavelengths apart so we would say in this case that the phase difference is λ/4 in distance, or 90 degrees or π/2 radians, since the whole wavelength part on its own would have no net effect whereas the additional quarter does matter. What the "detector then sees" depends critically on the precise value of this phase difference: If the phase difference is a whole number of wavelengths in distance (or 2 n π radians, where n = an integer) then constructive interference occurs; if the phase difference is half a wavelength in distance then destructive interference occurs; all intervening cases are also possible - if you are not familiar with the idea of constructive and destructive interference then click here for an explanative diagram.

The mathematical equation that summarises the whole situation above will not be obvious to non-mathematical students since it uses both vector algebra and complex numbers. Even if you cannot understand the mathematical details, it is still beneficial to follow the argument in a qualitative way: It can be shown by the use of vector scalar products that the phase difference in the above figure is 2πS.r (in radians) where r is the (vector) separation between the two electrons responsible for the double scattering. Next, this difference is translated into a wave relationship by the use of either a sine or cosine function, but as a final mathematical twist the complex number form of Demoivre's theorem is normally used to represent a cosine (the real part) or sine (the imaginary part) function. The final result is expressed as:

F(S) = e^{2π i
S.r}
where F signifies the amount of scattering (which is a function of both wavelength and angle 2θ in that S equals 2 sinθ / λ) arising from the phase difference between the upper and lower scattered waves.

Course Material Index

Section Index

Author(s): Paul Barnes
Simon Jacques
Martin Vickers