 |
Anomalous Scattering |
 |
Anomalous Scattering |
![]() The table of dispersion correction values is reference material.
The table of dispersion correction values is reference material.
Anomalous Scattering
The previous discussion made the assumption that the energy of the incident radiation was far away from any of the absorption energies of the atom. The theory of X-ray scattering by the electrons of an atom requires modification when this condition is no longer satisfied. It was shown (in an earlier section) that when copper X-ray radiation is used in conjunction with an iron sample, the phenomenon of X-ray fluorescence may be observed.
The phenomenon of X-ray fluorescence is due to absorption of an X-ray photon with simultaneous ejection of an electron whose energy level is similar to that of the incident energy of the photon. This is immediately followed by an outer electron filling the hole with the emission of an incoherent X-ray photon, the latter appearing as background noise in the diffraction data.
Not only do the iron atoms fluoresce when irradiated with X-rays produced from a copper anode, but their scattering factor is also modified according to the commonly used equation:
This modification to the scattering factor is commonly refered to as "anomalous scattering". However, it is more correctly called a dispersion effect since it depends (in a predictable way) upon the incident wavelength. The additional real and imaginary terms in the expression for the X-ray scattering factor above with components Δf′ and Δf′′, respectively, are more correctly called dispersion corrections since there is nothing anomalous about them. The table below lists some values (in electrons) of the dispersion corrections for a few elements for Cu Kα radiation, while the figure displays the values as a function of atomic number, Z:
| Element | C | Si | V | Fe | Co | Ni | Gd | Pb |
| Z | 6 | 14 | 23 | 26 | 27 | 28 | 64 | 82 |
| Δf′ | 0.017 | 0.244 | 0.035 | -1.179 | -2.464 | -2.956 | -9.242 | -4.818 |
| Δf′′ | 0.009 | 0.330 | 2.110 | 3.204 | 3.608 | 0.509 | 12.320 | 8.505 |
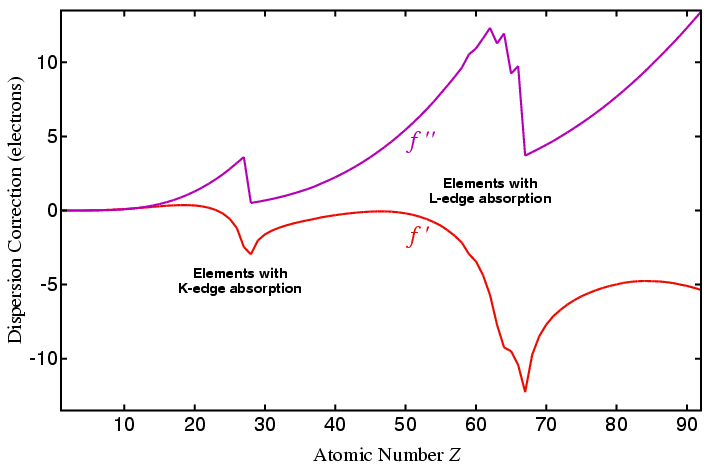
From the above, you should observe that the dispersion corrections are almost insignificant for the lighter elements, but are very significant for heavier elements, especially when the incident radiation is close to one of the K or L absorption edges of the element. Note that the imaginary term increases steadily in value up to the absorption edge, and then rapidly drops after the edge, while the real term at first increases, and then goes negative in value. The imaginary term provides the phase shift of the scattered X-ray photon.
In theory, the dispersion corrections depend on both the X-ray wavelength λ and the scattering angle θ. However, the dependence on the scattering angle is very small since the phenomenon results from the interaction of an incident X-ray with a core electron, and so in practice the terms Δf′ and Δf′′ are treated as constants for a given wavelength.
![]() Values for the dispersion correction have been tabulated for the common
laboratory X-ray wavelengths in the International Tables for
Crystallography,
Volume C, pages 219-222 (or in the old Volume IV, pages 149-150).
They can be also calculated for other arbitrary wavelengths (e.g. as used at
synchrotron sources) using the formulae by Cromer and Liberman.
Values for the dispersion correction have been tabulated for the common
laboratory X-ray wavelengths in the International Tables for
Crystallography,
Volume C, pages 219-222 (or in the old Volume IV, pages 149-150).
They can be also calculated for other arbitrary wavelengths (e.g. as used at
synchrotron sources) using the formulae by Cromer and Liberman.
| © Copyright 1997-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |