|
Scattering of X-rays by 2- and 3-Dimensional
Units |
 Course Material Index
Course Material Index
 Section Index
Section Index
 Previous Page
Previous Page
 Next Page
Next Page
Scattering of X-rays by 2- and 3-Dimensional
Units
We now move quickly up in dimension towards a 3D-crystal. Clearly the next case
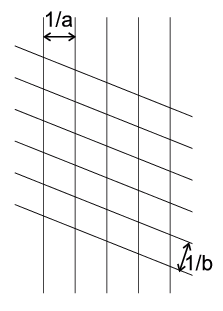
will be a two-dimensionally repeating set of scatterers as below:
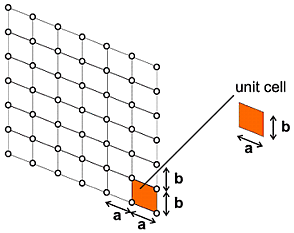
2D crystal (a, b repeats) :
von Laue condition S.a = h :
von Laue condition S.b = k :
The pattern repeats in two dimensions, the unit displacements being a
and b respectively and the unit parallelogram formed (indicated) being
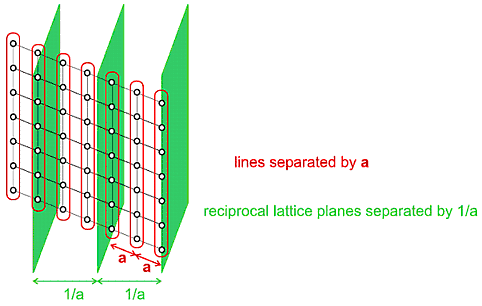
known as the unit cell. The second version of the above diagram shows how we
can re-visualise this so that atoms are grouped into rows of atoms spaced by
a. From the arguments used in the previous section this would lead to a
von Laue condition of a.S = h,
which is equivalent to a set of parallel reciprocal lattice planes spaced by
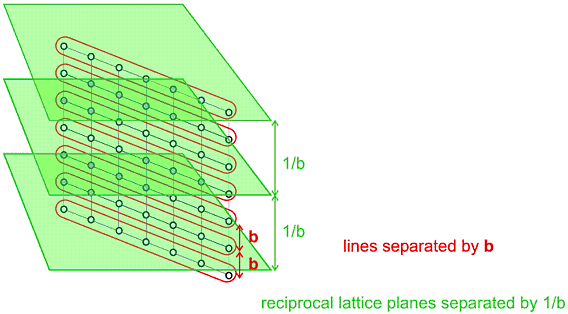
1/a. However the third version of the above diagram indicates that we
can alternatively visualise a different grouping of atoms, into rows spaced by
b, which then leads to an alternative von Laue condition
(b.S = k, say, an other integer)
and an alternative set of parallel reciprocal lattice planes spaced by
1/b.
If then the 2-dimensional crystal leads to these two alternatives, we must say
that both von Laue conditions must be simultaneously satisfied (i.e. two
integers, say h and k, involved). Since diffraction will only
occur when the reciprocal lattice planes intersect the Ewald sphere, yet we
have two sets of reciprocal lattice planes begging this condition, then the
only region where this "double condition" might be satisfied is where these two
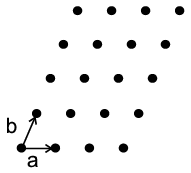
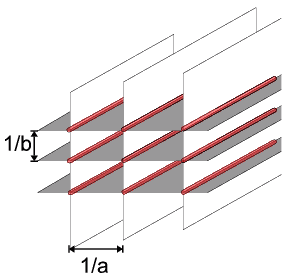
sets of planes intersect themselves and the Ewald sphere. Now two sets of
parallel planes intersect as a set of parallel lines (see below) which
themselves will intersect the Ewald sphere:
The 3D-crystal is the next and last case; it gets somewhat difficult to draw
though it is obvious that the above 2D arguments can be extended to 3D with the
result that:
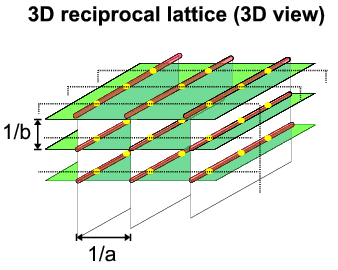
- in 3D, the unit cell is the solid parallelepiped formed by the sides
a, b and c.
- 3 simultaneous von Laue conditions need to be satisfied:
-
S.a = h, an integer
S.b = k, a second integer
S.c = l, a third integer
- the effective reciprocal lattice points must reside at the intersection of
3 sets of parallel planes. Three sets of parallel planes intersect as a lattice
of points, known as reciprocal lattice points and shown above in
yellow.
So there we have it: A three-dimensional crystal will diffract when the
experimental geometry is such that one (or more) of its reciprocal lattice
points intersects the Ewald sphere
(radius 1/λ). The reciprocal lattice
points will lie at the intersection of 3 sets of equidistant parallel planes
which are angled perpendicular to the a-, b- and c-
directions. For further explanation of the concepts of the Ewald sphere and the
reciprocal lattice click here.
 Course Material Index
Course Material Index
 Section Index
Section Index
 Previous Page
Previous Page
 Next Page
Next Page