 |
Further Interpretations of Diffraction |
Course Material Index
Section Index
Previous Page
Next Page
Further Interpretations of Diffraction
It is time now to bring together many observations on diffraction. We start with
the three von Laue conditions (equations on previous page) which define when
diffraction occurs. It so happens that these same three conditions together
also define a geometrical plane in the crystal which intersects the three axes
by amounts a/h, b/k and c/l
respectively (see below, in the example given
h = k = l = 2):
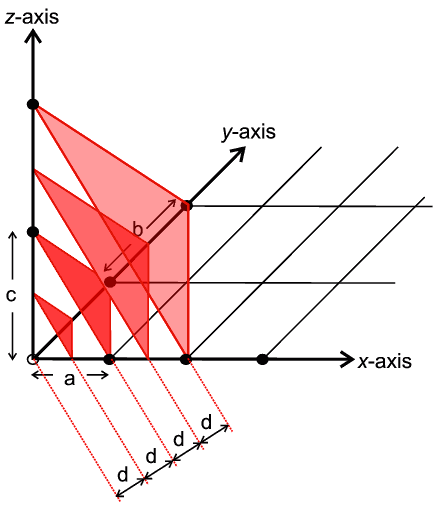Further this plane is at a distance d which is equal to 1/S from
the origin O. We can imagine a whole set of parallel planes, as indicated in
the Figure, in which each plane is separated from the next by d. We then
say that such a set of planes are characterised by these three indices
h,k,l. In fact the planes are invariably referred to as
Bragg planes (after Bragg) and the indices as Miller indices (after such a
system devised by Miller in 1839); the Miller indices often appear as a
subscript, e.g. dhkl meaning the d spacing between the
set of planes defined by h,k,l (for more notes on Miller
indices you can click here).
However the planes h,k,l have further significance.
Combining the knowledge that d = 1/S and
that S = 2 sin θ/λ
gives rise to the equation:
which is almost identical to the famous Bragg's law:
Thus we now have a simple rigorous equation, that any student should be able to
use to predict when diffraction will occur. The only difference between the two
is that the lower one also caters for higher orders of diffraction
(n>1) which is not so important here. We might also wonder whether
there can be any further significance to the Miller planes
(h,k,l) which so far only appear to be involved in
diffraction by the mathematical accident that their equation happens to be
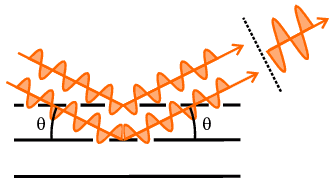
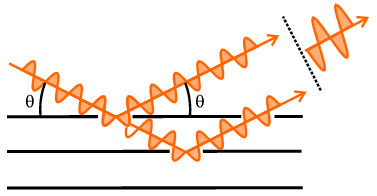
equivalent to the (von Laue) conditions for diffraction. In fact a diagram
which is well known to most science students (in two forms given below),
usually accompanying the mention of Bragg's law, brings out another feature:
From the geometry of either version in the above diagram, it can be easily
shown that the difference in path length of two X-ray beams scattered from
points in successive planes would amount to 2 d sin
θ. So another interpretation of Bragg's law is that it represents
the condition that the path difference between these two X-ray beams equals a
whole wavelength (or by higher multiples if n>1); of
course we know that when two interfering waves differ in phase by exactly one
wavelength, then they are effectively in-phase and will interfere
constructively. This notion has clearly served crystallography well over the
past 80-90 years with crystallographers strongly associating a given
h,k,l diffraction with the h,k,l
planes and their separation, d. This association has been strengthened
further by the popular use of terms such as "reflection by a set of
h,k,l planes" to describe diffraction under a
h,k,l set of von Laue conditions. However there is a
negative side to this balance sheet: many crystallography students have come
away with the incorrect notion that X-rays are actually reflected by
these Bragg h,k,l planes. This is of course nonsense,
given that the planes are abstract mathematical items and therefore are not
capable of "reflecting" anything; any student who has read this section should
realise at least by now that diffraction is a product of the scattering
of X-rays by atoms (with their electron clouds). It just so happens that
this multiple atomic scattering process occurs at the same instant that
projected path differences from Bragg planes equal a whole number of
wavelengths. As a student of this course we hope you will be able to use the
convenience of the notation of Bragg diffracting planes without believing that
they really reflect: always remember, planes are virtual but atoms are
real.
Course Material Index
Section Index
Previous Page
Next Page
