 |
Reflection Conditions
II. Screw Axes |
 |
Reflection Conditions
II. Screw Axes |
Screw Axes
Consider the effects of a twofold axis parallel to the c-axis direction of a crystal as shown schematically below:
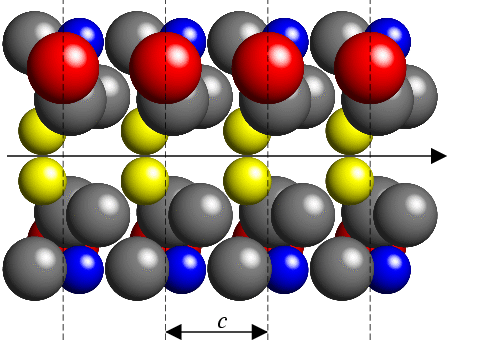
(001) planes perpendicular to the axis are shown as dashed lines. For these planes, and any other (00l) planes, symmetry-related molecules above and below the line of the 2-fold rotation axis (in the diagram above) will scatter the X-rays in phase with each other; hence there is no reflection condition for this symmetry element. This is illustrated in the schematic of reciprocal-space shown below, in which all reflections of the type 00l are present:
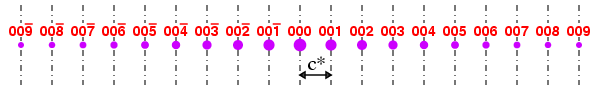
Contrast this with the case below which has the same unit-cell spacing along the c-axis direction as above, but which now has a two-one screw axis parallel to c:
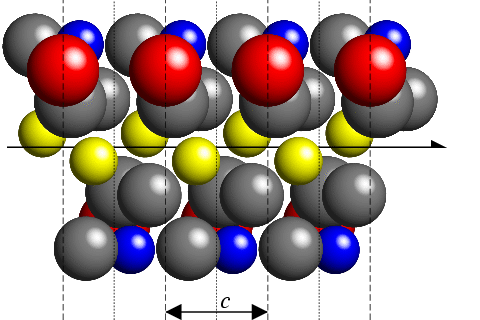
(001) planes perpendicular to the axis are still shown as dashed lines. In contrast to the previous case, the screw axis results in symmetry-related molecules exactly halfway between these planes as shown by the dotted lines. X-rays scattered from molecules on the dashed line will be exactly out of phase from those molecules on the dotted line giving a net zero intensity to the 001 reflection, i.e. the 001 reflection will be extinct.
Another way of looking at the same picture is to consider the lattice repeat distance as only 1/2 c for (001) planes since the only difference in the coordinates of symmetry-related molecules when projected onto the symmetry axis is 1/2 c. Halving the distance in real space doubles the distance in reciprocal space as shown below: thus reflections will only be observed at double the distance along the c*-axis direction at the reciprocal lattice points 002, 004, 006, etc., which corresponds to the reflection condition 00l: l = 2n. This is shown in the second schematic of reciprocal-space shown below. Note the missing reflections of the type 00l with l odd and that, effectively, the spacing of these observable reflections is twice c*.

As with the case of centred lattices, it is the translational component of the symmetry elements which gives rise to the reflection condition. Screw axes which have translation along a line only result in reflection conditions along a line in reciprocal space. This is shown in the table below:
| Screw Axis | Axis Direction | Reflection Conditions |
|---|---|---|
| 21 | a // a* | h00: h = 2n |
| 21 | b // b* | 0k0: k = 2n |
| 21 | c // c* | 00l: l = 2n |
| 31 or 32 | c // c* | 00l: l = 3n |
| 41 or 43 | c // c* | 00l: l = 4n |
| 42 | c // c* | 00l: l = 2n |
| 61 or 65 | c // c* | 00l: l = 6n |
| 62 or 64 | c // c* | 00l: l = 3n |
| 63 | c // c* | 00l: l = 2n |
From the table, it can be seen that if the translation component of the screw symmetry operator is 1/m, then the reflection condition is of the form m×n. Also, in contrast to the reflection conditions arising from a centred lattice, the reflection conditions here only apply to a small 1-dimensional class of reflections.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |