Reflection Conditions III. Glide Planes

Course Material Index  Section Index  Previous Page Next Page

The d-glide plane information given in the table below is reference material.

Glide Planes

It has already been shown that the translational component to the symmetry operator can give rise to reflection conditions for certain classes of reflection. The "1-dimensional" screw axes have a 1-dimensional reflection condition; likewise the "3-dimensional" centred lattice have a 3-dimensional reflection condition; therefore you should not be surprised to find out that glide planes, which are basically 2-dimensional, have a 2-dimensional type of reflection condition, i.e. they affect reflections in a zone plane.

As with the rotation axes discussed on the previous page, mirror planes do not give rise to reflection conditions: there is no translational component to the symmetry operator in this instance. Glide planes do give rise to reflection conditions as illustrated in the figure below:

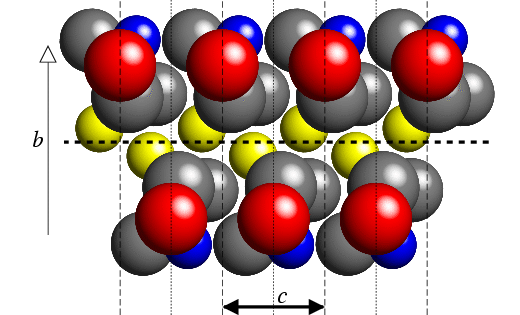
The figure shows a c-glide plane perpendicular to the b axis. As with the two-one screw axis, the effective halving of the unit cell along the c-axis direction leads to the reflection condition l = 2n for a particular class of reflection: in contrast to the screw axis, it is all of the zone plane h0l that is affected by this symmetry element, and not just reflections of the type 00l. This is illustrated in one of the figures shown earlier used to demonstrate the Laue symmetry of a single crystal:

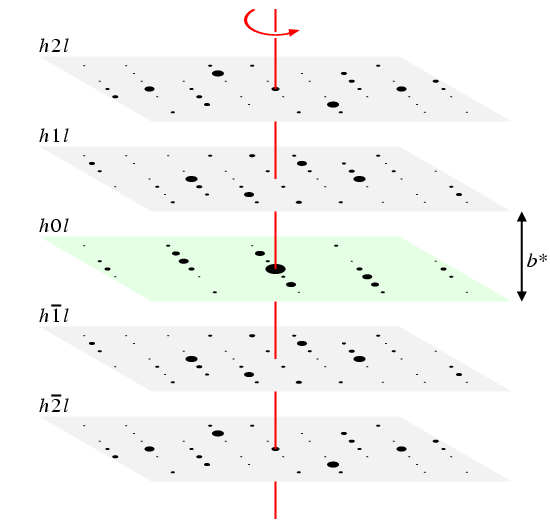
In the above figure, it should be obvious that the zone plane shown in pale green has fewer reflections than the non-zone planes along the b-axis direction. The h0l plane is shown below with the position of the extinct reflections circled in green:

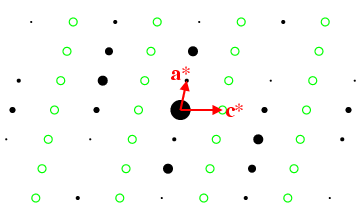
From this diagram, you should be able to see that the effective halving of the real-space distance along c due to the c-glide plane leads to an affective doubling of distance along c* within the zone plane h0l. Hence the reflection condition for a c-glide plane perpendicular to the b axis is h0l: l = 2n.

As discussed in the first section on symmetry, there are many types of glide plane and these lead to a variety of reflections conditions. A listing of the glide planes that can occur in the monoclinic and orthorhombic crystal systems is given in the table below, together with the reflection conditions associated with them:

Glide Plane	Symmetry Operator	Reflection Condition
b x	T-x,1/2+y,z	0kl: k = 2n
c x	T-x,1/2+y,z	0kl: l = 2n
n x	T-x,1/2+y,1/2+z	0kl: k + l = 2n
d x	T-x,1/4+y,1/4+z	0kl: k + l = 4n
a y	1/2+x,T-y,z	h0l: h = 2n
c y	x,T-y,1/2+z	h0l: l = 2n
n y	1/2+x,T-y,1/2+z	h0l: h + l = 2n
d y	1/4+x,T-y,1/4+z	h0l: h + l = 4n
a z	1/2+x,y,T-z	hk0: h = 2n
b z	x,1/2+y,T-z	hk0: k = 2n
n z	1/2+x,1/2+y,T-z	hk0: h + k = 2n
d z	1/4+x,1/4+y,T-z	hk0: h + k = 4n

From the table, a pattern emerges: when the glide plane is perpendicular to a (i.e. x), the zone plane affected is 0kl, when it is perpendicular to b, the zone plane affected is h0l, and when it is perpendicular to c, it is in the hk0 zone plane that the reflection condition may be observed. Likewise, a-glide planes give rise to reflection conditions of the type h = 2n, b-glide planes give rise to k = 2n, and c-glide planes give rise to l = 2n, while the diagonal n-glide planes result in reflection conditions in which the sum of the two indices is even. Note that this table is not exhaustive and that the effect of certain glide planes in high-symmetry space groups has been omitted.

The discussion so far has concentrated on reflection conditions as observed in single-crystal data sets. The next question is how to use this information to determine space group symmetry, and for this an understanding is required of the differences between single-crystal and powder diffraction data with respect to symmetry observation.

Course Material Index  Section Index  Previous Page Next Page