 |
Space-Group Determination in Practice |
 |
Space-Group Determination in Practice |
![]() The space-group totals in the first table are for reference only;
likewise, the contents of the second and third tables.
The space-group totals in the first table are for reference only;
likewise, the contents of the second and third tables.
Space-Group Determination in Practice
Getting Started
Space group determination from powder data should not be compared to the automatic procedures available in single-crystal programs (such as XPREP in the SHELX suite of programs). The basic reason for this is that the 1-dimensional powder data set intrinsically contains less symmetry information that an equivalent 3-dimensional single-crystal data set. Usually the aim is to determine the most likely space groups consistent with the powder diffraction data rather than a unique solution: starting with the maximum 230 possible space groups (as listed earlier), the aim is to reduce this number to just a few.
As mentioned previously, the first step is the determination of the unit-cell geometry. This narrows the 230 space groups down as follows:
| Unit-Cell Geometry | Inferred Crystal System(s) | No. of Space Groups |
|---|---|---|
| a ≠ b ≠ c and α ≠ β ≠ & gamma; & ne; 90° | Triclinic | 2 |
| a ≠ b ≠ c and α = γ = 90° and β ≠ 90° | Monoclinic | 13 |
| a ≠ b ≠ c and α = β = γ = 90° | Orthorhombic | 59 |
| a = b ≠ c and α = β = γ = 90° | Tetragonal | 68 |
| a = b = c and α = β = γ ≠ 90° | Trigonal (Rhombohedral) | 7 |
| a = b ≠ c and α = β = 90° and γ = 120° | Trigonal or Hexagonal | 45 |
| a = b = c and α = β = γ = 90° | Cubic | 36 |
The next step is to find out whether any reflection condition exist: firstly
for centred lattices, then for glide planes, and lastly for screw axes.
Care must be taken to distinguish different reflection conditions. For example,
a C centred monoclinic lattice will exhibit the
general reflection condition
Suppose the unit-cell geometry indicates that the most likely space group is monoclinic. Is it possible to then deduce from the reflection conditions the precise space group? The table below shows the reflection conditions that can be observed for the monoclinic crystal system and the conclusions that can be drawn from them:
| Reflection Condition(s) | Possible Space Group(s) | ||||||
|---|---|---|---|---|---|---|---|
| None | → | P2 | (3) | ||||
| Pm | (6) | ||||||
| P2/m | (10) | ||||||
| 0k0: k = 2n | → | P21 | (4) | ||||
| P21/m | (11) | ||||||
| h0l: l = 2n | → | Pc | (7) | ||||
| P2/c | (13) | ||||||
| h0l: l = 2n and 0k0: k = 2n | → | P21/c | (14) | ||||
| hkl: h + k = 2n | → | C2 | (5) | ||||
| Cm | (8) | ||||||
| C2/m | (12) | ||||||
| hkl: h + k = 2n and h0l: l = 2n | → | Cc | (9) | ||||
| C2/c | (15) | ||||||
| h0l: h = 2n | → | Pa | (7) | ||||
| P2/a | (13) | ||||||
| h0l: h + l = 2n | → | Pn | (7) | ||||
| P2/n | (13) | ||||||
| h0l: h = 2n and 0k0: k = 2n | → | P21/a | (14) | ||||
| h0l: h + l = 2n and 0k0: k = 2n | → | P21/n | (14) | ||||
| hkl: k + l = 2n | → | A2 | (5) | ||||
| Am | (8) | ||||||
| A2/m | (12) | ||||||
| hkl: h + k + l = 2n | → | I2 | (5) | ||||
| Im | (8) | ||||||
| I2/m | (12) | ||||||
| hkl: k + l = 2n and h0l: h = 2n | → | Aa | (9) | ||||
| A2/a | (15) | ||||||
| hkl: h + k + l = 2n and h0l: h = 2n | → | Ia | (9) | ||||
| I2/a | (15) | ||||||
The top part of the table shows the deductions that can be made if the unit cell matches the space group in its so-called standard setting (see below). There is no a priori reason why this should be so; thus reflection conditions corresponding to the non-standard settings of the various space groups are given in the bottom part of the table. However, the main point to note here is that only one set of reflections leads to a unique choice of space group, i.e. to space group number 14: crystallographers are fortunate that the most frequently-occuring space group has a unique set of reflection conditions! All of the other reflections imply a non-unique solution for the determination of space-group symmetry in the monoclinic crystal system.
The above discussion is a little theoretical, so to see how space-group symmetry is determined in practice, a case study will be given on the following page.
Standard & Non-Standard Settings
When a powder diffraction pattern is indexed and a refined unit cell is extracted from the data, then the axes of the unit cell are labelled somewhat arbitrarily, though always as a right-handed set. Once the space-group symmetry is determined, it is often convenient to relabel the unit-cell axes so that certain symmetry elements are always positioned in the same direction. For example, if the symmetry elements are a primitive monoclinic lattice with a two-one screw axis perpendicular to a glide plane, then the material has space group number 14. However, depending on the labelling of the axes (and sometimes the choice of unit cell), the space-group symbol can be P21/a, P21/c, or P21/n, which are all different settings of the same space group.
This is demonstrated in the three figures below. These show a section of the ac plane of a monoclinic lattice, where the sole symmetry element is a glide plane with the direction shown by the grey arrow. The origin in each case is indicated by the letter "O" and three unit cells have been highlighted. In each case the b axis comes out of the plane of the screen so as to form a right-handed set with a and c:
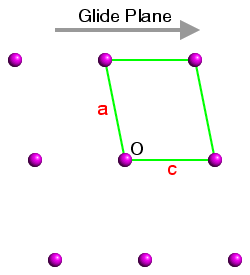
Space Group No. 7 Pc Figure 1 |
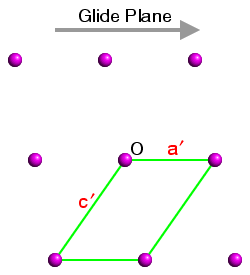
Space Group No. 7 Pa Figure 2 |
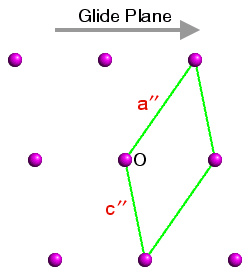
Space Group No. 7 Pn Figure 3 |
The space-group symmetry is identical for each figure, but the space-group symbols for figures 1 to 3 are Pc (the standard setting), and Pa and Pn (two non-standard settings). In figure 1, the glide plane direction is parallel to c; in figure 2, it is parallel to a′ and in figure 3, it is parallel to the diagonal of the unit cell. Hence the space-group symbols Pc, Pa, and Pn, respectively.
Given the possibility of different setttings, crystallographers often prefer to use just one setting, known as the standard setting, so that direct comparisons between crystallographic information is possible. In powder work, the use of non-standard settings is often more common than in single-crystal experiments: the most common reason is that powder experiments are often used to study phase transitions, when it is often more convenient to work with similar unit cells above and below the phase-transition temperature. You should also be aware that non-standard settings can also involve the use of different origins as well as different unit cells.
Problems & Special Cases
Enantiomorphic space groups present particular difficulties with powder diffraction since it is impossible to determine absolute configurations within a crystal due to the 1-dimensional nature of the data. It is important to remember this when working with many organic materials, especially those derived from natural products (e.g. sugars and amino acids).
Also reflection conditions are not unique for each type of screw axis. In particular note that right- and left-handed screw axes with the same degree of rotation and translation have the same reflection conditions, e.g. 31 and 32, 41 and 43. This implies that certain pairs of space groups, confusingly known as enantiomorphic pairs, cannot be distinguished. The enantiomorphic pairs are listed in the table below:
| Right-handed | P31 | P3121 | P3112 | P41 | P4122 | P41212 | P61 | P62 | P6122 | P6222 | P4132 |
| Left-handed | P32 | P3221 | P3212 | P43 | P4322 | P43212 | P65 | P64 | P6522 | P6422 | P4332 |
The above discussion may still seem a little theoretical, so to see how space-group symmetry is really determined in practice, a case study is now given to demonstrate the process on a step-by-step basis.
![]()
Footnote:
Other problem pairs are the orthorhombic space groups I222 and
I212121
and the cubic space groups I23 and
I213, both pairs possessing the
same symmetry elements, but with the symmetry elements
located differently within each pair in 3-dimensional space.
| © Copyright 1997-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |