Case Study

Course Material Index  Section Index  Previous Page

Case Study

A case study is now given to demonstrate space-group determination in practice using a measured data set. The structure was originally unknown so this case study provides a real example of how to proceed in practice.

The powder diffraction data shown below (in purple) is of a sample of the Freon gas fluoro-trichloromethane condensed to a solid at 1.5 K and measured on an angle-dispersive neutron diffractometer with λ = 1.594 Å. The pattern was indexed (with hkl shown in red) as orthorhombic with a = 15.51 Å, b = 5.88 Å, and c = 9.53 Å. You should notice that the diffraction pattern has few peaks below about 19°, but then many thereafter.
This is made clearer when the position of all possible peaks for this unit cell is calculated () as shown in the line diagram shown below the data:

Line positions generated assuming space-group symmetry Pmmm

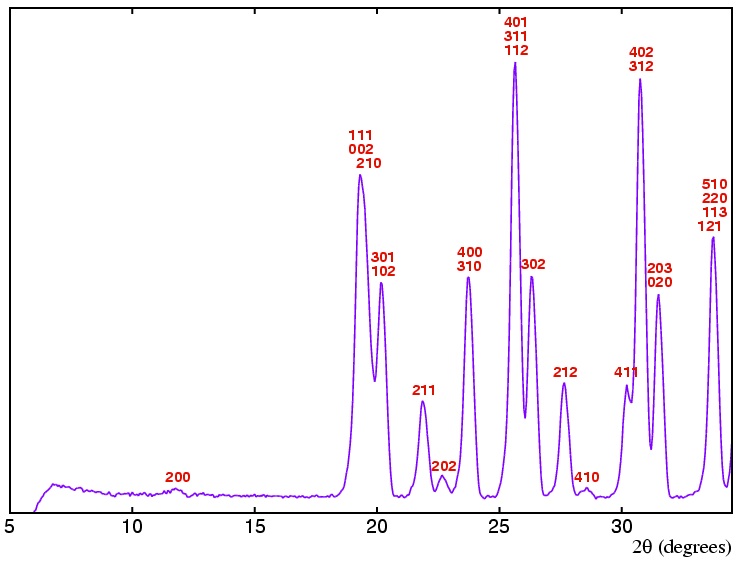
The most obvious problem is that many of the peaks consist of overlapping reflections: this is a reality that one has to face with most powder-diffraction data (unless one is lucky enough to have access to the highest-resolution powder diffractometers at third-generation synchrotron sources).

The first step is to determine the absence or presence of any lattice reflection conditions. The presence of certain reflections can be used to determine the answer. It is important to consider reflections that do not have all even integer Miller indices. Thus the presence of the 202 reflection provides no symmetry information whatsoever. The presence of the 211 reflection positively tells us that the lattice cannot be B centred since h + l is odd and this would break the reflection condition hkl: h + l = 2n that applies to a B-centred lattice. If the lattice is not B centred, then neither can it be F centred. Additionally, the presence of this reflection tells us that the lattice cannot be C centred since h + k is also odd. The 211 reflection provides no symmetry information about whether the lattice is A or I centred. The presence of the 212 reflection, where both k + l and h + k + l are odd, indicates that the lattice is neither A nor I centred: hence the space group must be primitive, and probably primitive orthorhombic.

The next step is to look for glide planes. As before, many of the reflections that one would like to consider, i.e. those on zone planes where one of hkl indices is zero, are severely overlapped. Using reflections that are present such as the 410 still provide useful symmetry information: in this instance, both k and k + l are odd indicating that if there is a glide plane perpendicular to c then it cannot be either a b or n (or d). Likewise considering the 302 reflection, h and h + l are odd indicating that if there is a glide plane perpendicular to b then it cannot be either an a or n (or d). There are no suitable reflections (at least in the range of data shown here) to examine to test whether glide planes perpendicular to a are absent or not.

The final step is to look for zone-axis reflections that break the two-one screw axis reflection condition. There are none present so no conclusions can be drawn here. The possibilities for the symmetry elements present are summarized in the table below:

The above table still leaves many possibilities for the space group. However, given that molecules pack better in the presence of glide planes than with mirror planes, it is reasonable to assume that the most likely space group is one in which there is a c-glide plane perpendicular to y and an a-glide plane perpendicular to z. With this assumption, then one can generate the line diagram below:

Line positions generated assuming space-group symmetry P?ca

This line diagram is now beginning to look a better match to the observed diffraction data. But the space group is still not known, so how does one proceed further? The space group symbol must be of the form P?ca so it is only a question of determining the symmetry element(s) with respect to the x-axis direction. Space group tables are very useful at this point. If the crystal structure is non-centrosymmetric, then the only possible space group is P2₁ca. Possible centrosymmetric space groups to be considered are Pmca, Pcca, Pnca, and Pbca. Thus from the diffraction data shown here it is possible to deduce that the space group symmetry of solid fluoro-trichloromethane is one of five possible space groups.

Is it possible to take the analysis any further? The answer is yes, but the best method for doing this will not be described at this point. One possibility is to consider the list of space-group frequencies: while this is likely to save you time on average by indicating the most probable solution, the molecules in your crystal structure may prefer to pack in a less-commonly observed space group! Naturally, the true answer is only obtained once the crystal structure has been solved and successfully refined, but that is another story.

Footnote:
The actual space-group symmetry in this instance is Pbca, for which a reflection list may be generated for comparison with the diffraction data. Click here if you want to see the match.

Course Material Index  Section Index  Previous Page