Symmetry Diagrams I. Flat Projection

Course Material Index  Section Index  Next Page

Flat Projection

So far you have seen examples of 3-dimensional symmetry elements and their associated symmetry operators. Before discussing how these symmetry elements can be combined to form point groups and space groups, it is useful to consider how objects related by symmetry can be projected onto a plane. The reason for this is to make the symmetry relationship between objects obvious to the human eye. That the human eye readily pictures symmetry in 2-dimensions compared to 3-dimensions can be demonstrated by considering a picture of a square versus that of a cube (assuming that the latter is not viewed from certain special positions).

Crystallographers generally use two types of projection. The simplest one is the flat projection similar to that used on large-scale maps where heights, e.g. of mountains, are shown by contours and/or by height values next to the marked position of, say, the peaks. This is illustrated in the diagram below for four objects that represent atoms, but which could equally-well represent the centre of gravity of molecules.

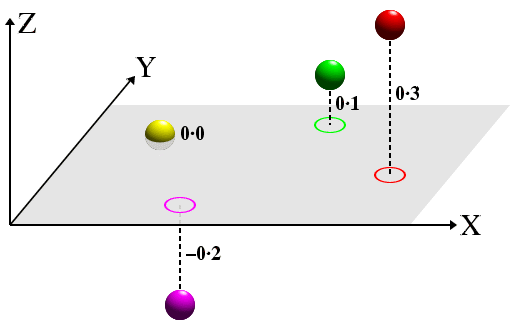
Notice that the lines of projection (dashed lines) are perpendicular to the projection plane (shown in grey). Atoms (or molecules) below the projection plane (i.e. with a negative z-coordinate) have a negative distance from the plane, while those above are positive. The equivalent 2-dimensional projection diagram, shown below, should be easy to relate to the equivalent 3-dimensional figure shown above.

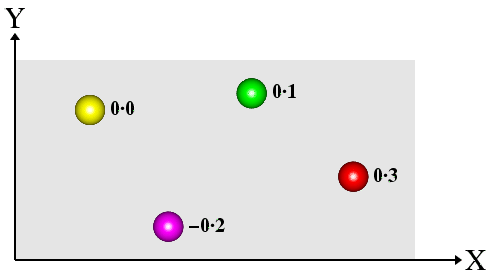
The heights have been marked directly against each atom on the projection plane. This type of projection is the one normally used to show the space-group symmetry of atoms/molecules within a crystal structure. It will be used extensively to explain the symmetry of different space groups later on in the course material.

Course Material Index  Section Index  Next Page