 |
Centred Space Groups |
 |
Centred Space Groups |
Centred Space Groups
So far, the only space considered in detail have been those with a primitive lattice, P. Centred space groups involve additional lattice translations in addition to those of the whole unit-cell lattice translations as exhibited by the simplest space group P1. A frequently observed centred space group is the monoclinic space group C2/c. The properties of this space group, which is shown below, will be used to demonstrate some of the properties that result from a C-centred lattice. By extension, similar properties arise from the other lattice centrings. You should note that there is no symmetry symbol in the diagram to indicate a centred lattice: however, the presence of it can be inferred from the combination of symmetry elements present as will be explained.
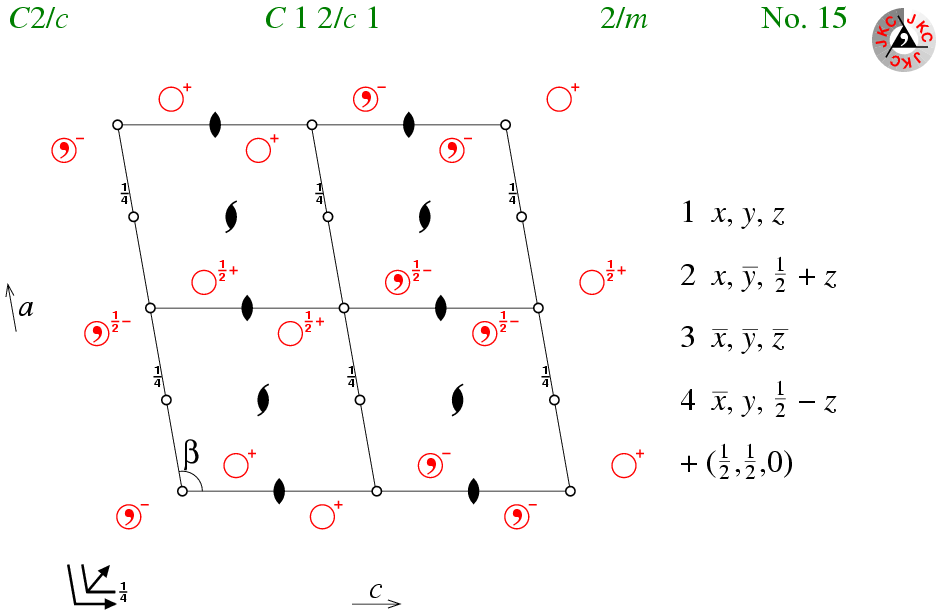
The space group C2/c can be considered as a combination of a C-centred lattice with space group P2/c (or alternatively space group P21/n).
Space group P2/c has an inversion centre at the origin plus 7 others per unit cell (as for space group P-1 as discussed earlier). Considering the inversion centre at the origin, then the combination of 1/2+x,1/2+y,z with -x,-y,-z yields the symmetry operator 1/2-x,1/2-y,-z, which corresponds to an inversion centre at the point (1/4,1/4,0) as shown in the figure. This approach can be extended to the other 7 inversion centres of the primitive space group, yielding a total of 16 per unit cell in the C-centred space group. These 16 should be considered as two groups of 8 since each set of eight is related as in P-1.
Furthermore, space group P2/c has a twofold rotation axis at (0,y,1/4) plus 3 others per unit cell (each separated by either half a unit cell in a or c similar to the two-one screw axes as discussed earlier). Considering the twofold rotation at (0,y,1/4), then the combination of 1/2+x,1/2+y,z with -x,y,1/2-z yields the symmetry operator 1/2-x,1/2+y,1/2-z, which corresponds to a two-one screw axis along the line (1/4,y,1/4) as shown in the figure. This approach can be extended to the other 3 rotation axes of the primitive space group, yielding a total of 4 screw axes per unit cell in the C-centred space group. Thus one consequence of the C-centred lattice is an equal number of twofold rotation axes and two-one screw axes.
Finally, considering the c-glide plane with symmetry operator x,-y,1/2+z, then the combination of this with the C-centring results in an n-glide plane located at y = 1/4 with symmetry operator 1/2+x,1/2-y,1/2+z. Thus, another consequence of the C-centred lattice is a set of interleaving planes, separated by 1/4. These can be seen more clearly in the final interactive exercise that follows in the projections as viewed down either the a or c axes.
Finally, an alternative view of this space group is a combination of the two primitive monoclinic space groups P2/c and P21/n, which generate a C-centred lattice translations when combined.
| © Copyright 1995-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |