 |
Monoclinic Space Groups |
 |
Monoclinic Space Groups |
Monoclinic Space Groups
The combination of the symmetry properties of space group P1 with either a twofold rotation axis, two-one screw axis, mirror plane, or glide plane, or a combination of them provides a derivation for the 13 monoclinic space groups. As with the triclinic space groups, certain general principles will be established here. The presence of a symmetry element of order 2 forces two of the unit cell angles to be 90° as shown earlier. By convention the unique axis direction, i.e. the one parallel to the symmetry axis and/or to the normal of the symmetry plane is defined as the b axis, with the angle that is not contrained to be 90° being β, ideosyncratic though this may be. (In the tetragonal, trigonal, and hexagonal crystal systems the unique axis is conventionally chosen as c.)
Since it is the most frequently-occurring space group, P21/c will be used throughout this section to illustrate some of the properties of the monoclinic space groups. Its space-group diagram, viewed down the b axis, is shown below:
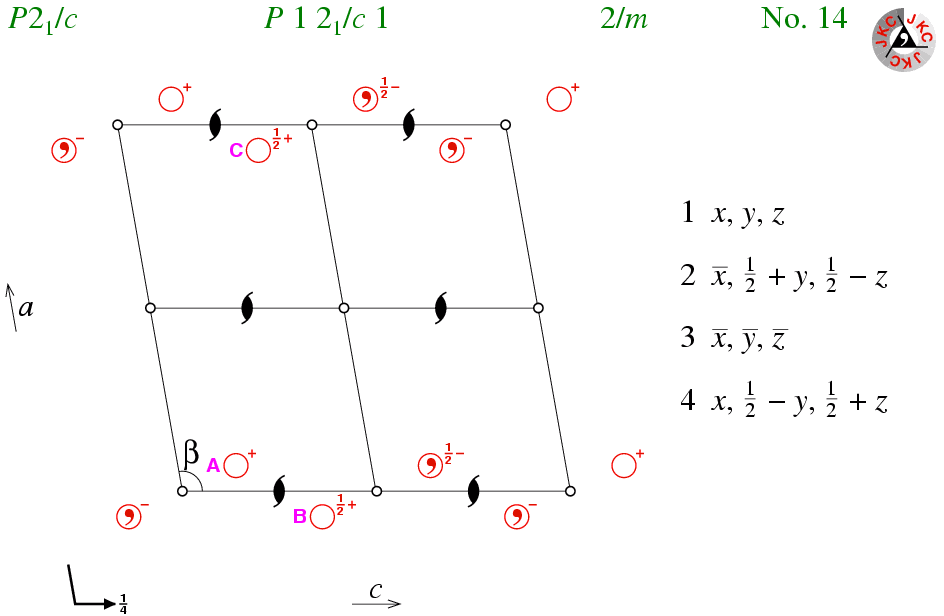
This space group has three types of symmetry element: two-one screw axes, glide planes, and points of inversion. The most convenient place for the origin is on a point of inversion; points of inversion fix the coordinates in each of the three dimensions, in contrast to say an origin on the two-one screw axis which fixes it only in two dimensions. Note that origin could be chosen at the intersection of a two-one axis and the glide plane, since this is also a fixed point in space, but it is a less convenient one. (In general, the origin is chosen to be at the point of inversion in centrosymmetric space groups since it simplifies the calculation of structure factors.)
Fixing the point of inversion at the origin implies that one of the
symmetry operators is -x,-y,-z. What are the symmetry
operators for the glide plane and screw axis? (The answer is clearly listed,
but suppose it was not given here!)
The symmetry operator for the c-glide plane
is of the form
x,T-y,1/2+z, while the symmetry operator
for the two-one screw axis is of the form
Given that there is a two-one screw axis at (0,y,1/4) with corresponding symmetry operator -x,1/2+y,1/2-z, then the question arises as to how many other ones are there in the unit cell. Consider the point with coordinates (0.07,+y,0.15) labelled A in the figure. If one applies the symmetry operator for the two-one screw axis with coordinates 0,y,0 to this point, then one obtains the point labelled B with coordinates (-0.07,1/2+y,0.35). The application of a single lattice translation parallel to a brings the point B to the position labelled C with coordinates (0.93,1/2+y,0.35). Point C is symmetry related to the initial point A by the two-one screw axis in the middle left-hand side of the unit cell with coordinates (1/2,y,1/4). Likewise, one can show by considering the effect of lattice translations parallel to c and to a plus c that likewise there must be two more screw axes within the unit cell with coordinates (0,y,3/4) and (1/2,y,3/4), respectively. To summarise, there are thus 4 two-one screw axes per unit cell in space group P21/c.
This concept of 4 two-one screw axes per primitive unit cell, each separated by one-half unit-cell lengths from each other, is one that extends to all two-one screw and twofold rotation axes in other space groups. Thus you will see 4 twofold rotation axes per unit cell in the space group diagram of the monoclinic space group P2, which may be formed by combining P1 with a twofold rotation axis.
The space group P21/c has 8 points of inversion, 4 two-one screw axes; how many c-glide planes do you think are present? As with the points of inversion and twofold rotation axes, the glide planes are also spaced out in 1/2 unit cell increments. In this space group, the symmetry operator x,1/2-y,1/2+z corresponds to a c-glide plane at y = 1/4 (shown by the bent arrow in the bottom left-hand corner of the diagram). If this is combined with a lattice translation along b, then one obtains the symmetry operator x,3/2-y,1/2+z, which corresponds to a c-glide plane at y = 3/4. You should be aware that although this plane cannot be shown easily in the space-group diagram it is implicitly present. Both glide planes will be seen in the space-group diagram when the view is down one of the a or c axes; these views are available in the clickable figure that follows this page.
|
© Copyright 1995-2006.
Birkbeck College, University of London.
|
Author(s):
Jeremy Karl Cockcroft Huub Driessen |