 |
Triclinic Space Groups |
 |
Triclinic Space Groups |
Triclinic Space Groups
There are only two triclinic space groups and these are given the symbols P1 and P-1; the former is enantiomorphic, while the latter is centrosymmetric. The lack of symmetry, other than 1 or -1 axes, in the triclinic space groups results in the complete absence of any symmetry constraint on the unit cell parameters as stated earlier.
Space group P1 is the "mother" of all space groups in that all space groups possess the symmetry elements of this space group. It is characterised by the complete absence of any rotation axes (other than the identity rotation axis of order 1), rotary-inversion axes, screw axes, or planes. The only symmetry elements that it possesses are the simple lattice translations along the a, b, and c unit-cell directions, written in symbolic form as t(1,0,0); t(0,1,0); and t(0,0,1).
The space group diagram for P-1 is shown below:
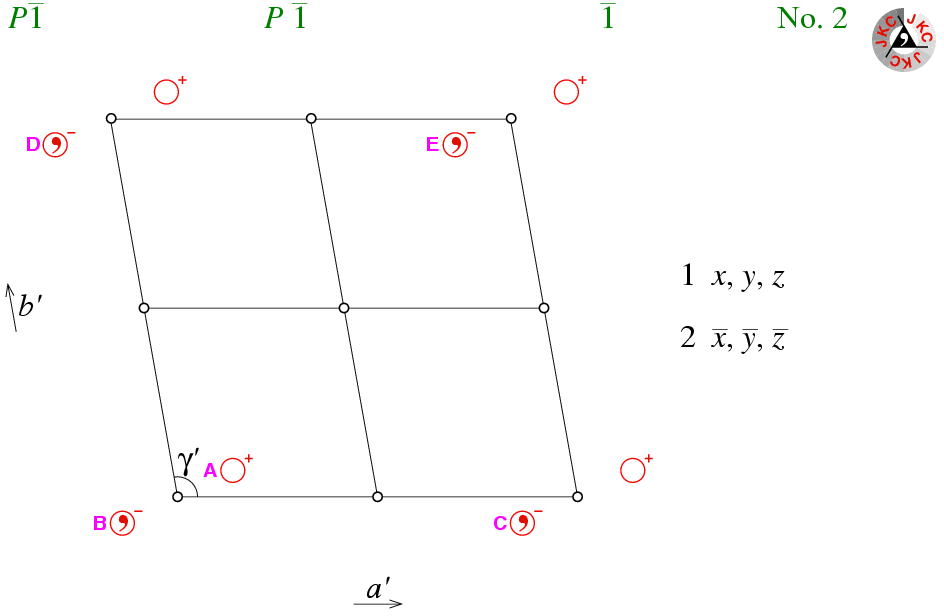
This space group diagram shows a projection down the c axis. Given that none of the unit cell angles are orthogonal by symmetry, the other two axes do not lie in the plane of the screen; this is indicated by the use of the prime character ( ′ ) on the labelling of the unit-cell axes. The same comment can be made regarding the unit-cell angle γ.
For space group P1, there is only one symmetry equivalent position within the unit cell; the associated symmetry operator being listed simply as x,y,z. For space group P-1, there are now two symmetry equivalent positions within the unit cell due to the presence of the point of inversion. It is convenient to choose the origin for this space group so that it coincides with the the point of inversion. Hence P-1 has a second symmetry operator listed as -x,-y,-z.
The combination of space group P1 with a point of inversion to form space group P-1 does not imply a single point of inversion per unit cell; far from it as shown in the figure above! Consider the point labelled A with coordinates x,y,z; it is symmetry related to the point labelled B by the point of inversion at the origin, which has the symmetry operator -x,-y,-z. Lattice translations of the point B along a brings it to the point labelled C; along b brings it to the point labelled D; and along a and then b brings it to the point labelled E. Thus the symmetry operators which symmetry relate point A to points C, D, and E are 1-x,-y,-z; -x,1-y,-z; and 1-x,1-y,-z, respectively. These three symmetry operators correspond to points of inversion at 1/2,0,0; 0,1/2,0; and 1/2,1/2,0, respectively, as shown in the space group diagram. Taking into account a translation along c leads to four more points of inversion within the unit cell. Thus there are 8 points of inversion per primitive unit cell as listed in the table below for space group P-1:
| Fractional Coordinates | 0,0,0 | 1/2,0,0 | 0,1/2,0 | 1/2,1/2,0 | 0,0,1/2 | 1/2,0,1/2 | 0,1/2,1/2 | 1/2,1/2,1/2 |
|---|---|---|---|---|---|---|---|---|
| Symmetry Operator | -x,-y,-z | 1-x,-y,-z | -x,1-y,-z | 1-x,1-y,-z | -x,-y,1-z | 1-x,-y,1-z | -x,1-y,1-z | 1-x,1-y,1-z |
Other points of inversion (e.g. the one at 1,0,0) lie in neighbouring unit cells. The principles learnt here can be applied to all primitive centrosymmetric space groups: they all have 8 centres of inversion, each separated by one-half a unit cell in each of the cell directions. In general, principles based on low-symmetry space groups will apply to the higher-symmetry ones, but not vice versa. Hence it is advantageous to understand the principles behind the low-symmetry space groups before trying to understand the principles underpinning the high-symmetry ones.
|
© Copyright 1995-2006.
Birkbeck College, University of London.
|
Author(s):
Jeremy Karl Cockcroft Huub Driessen |