 |
Scattering of X-rays by a Single Electron |
Course Material Index
Section Index
Next Page
Scattering of X-rays by a Single Electron
It is useful to consider the scattering of X-rays by an electron to be a
fundamental scattering process (later we will also consider the scattering of
neutrons). The unit of X-ray energy is termed an X-ray photon and can be
imagined as a finite travelling wave of electromagnetic displacement. Many of
the diagrams we will use will be highly schematic (and should not always be
taken too literally); the first diagram falls into this class, illustrating the
basic features of the electric displacement of an X-ray photon:
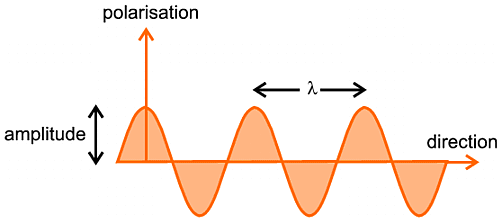The terms used are important: amplitude (the maximum displacement), wavelength
denoted by λ (the distance between successive maxima), direction of
propagation of the X-ray photon (horizontal from left to right as it appears on
your screen), and polarisation (the direction of electric displacement) which
appears vertical on your screen.
An X-ray can be scattered by an electron. This can be perceived by the change
in direction of the X-ray after it has "passed" the electron (so to speak), as
illustrated in the following schematic diagram:
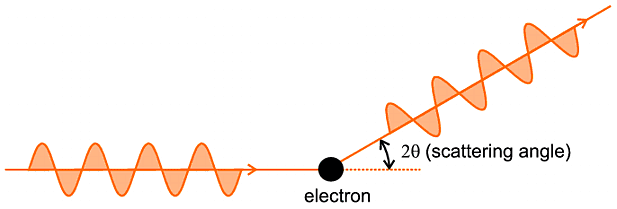Again this diagram is somewhat naive (and perhaps questionable on true quantum
mechanical grounds) but it gets the essential ideas over. It is not so
important to understand exactly what goes on as the X-ray interferes with and
is scattered by the electron, but the net end result is important: both the
direction and polarisation of the X-ray photon have been altered by an angle
2θ. There is nothing to worry about by the use of 2θ as the angle
of scattering (rather than, say, θ this is simply a matter of convention
at this stage. We might also point out that the X-ray photon also suffers a
phase shift of 180 degrees (π radians), but this is not important either at
this stage.
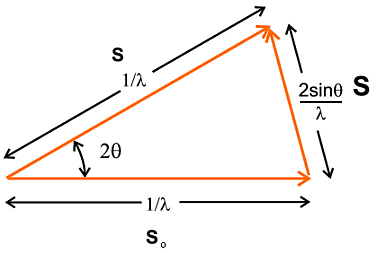
This whole process is often summarised by an important vector diagram and
accompanying vector equation, though you do not really need to understand much
about vector algebra to follow these: since a vector is something which has
both magnitude and direction we can represent two items, the absolute momentum
of the X-ray photon and its direction of propagation, by a vector. One other
fact you should accept is that the momentum of a wave is proportional to the
inverse of its wavelength (a result discovered earlier in the 20th century by
Planck); so we make the length of the vector equal to
1/λ and the direction of the vector the same as the
propagation direction of the X-ray. Then we represent the scattering event by a
vector diagram, which follows, in which so
represents the direction and momentum of the incident X-ray photon (i.e. before
it is scattered) and s represents the direction and momentum of the
X-ray photon after being scattered. An important aspect of diffraction is that
we only consider elastic scattering; by that we mean that there is no loss of
X-ray photon energy through scattering so that the energy (and absolute
momentum) of the X-ray photon remains unchanged. This is why the length of
s in the diagram (1/λ) has been made the same
as the length of so. Finally the vector
S, which bridges s and so,
represents the net change as a result of the scattering process and is an
important item, often referred to as the scattering vector S; its length
is equal to
2 sinθ / λ
(you might like to try proving this from the properties of the
isosceles triangle in the diagram).
The vector equation that summarises the above figure is:
s = so + S
which basically re-iterates that the scattered wave (s) is the result of
the incident wave (so) being subjected to the
scattering process (+ S).
Course Material Index
Section Index
Next Page