 |
Zone-Indexing Methods |
 |
Zone-Indexing Methods |
Zone-Indexing Methods
The methods that have been described so far work well for the higher-symmetry crystal systems, but are less suitable for the lower-symmetry ones. Zone indexing is a method that works extremely well for low-symmetry systems since it makes no prior assumptions about degrees of symmetry. Further tests are then required to check whether the low symmetry cell corresponds to a higher symmetry system, e.g. rhombohedral, trigonal, and hexagonal cells are nearly always indexed as monoclinic.
A zone is a plane in reciprocal space passing through the origin. In general 3 points in space are required to uniquely define a plane, but for a zone plane only 2 act as variable parameters, since the third point is fixed at the origin. Since the unit-cell axes can be arbitrarily chosen, one can choose 2 of the axes, say a and b, to be in the zone plane. Points in this plane therefore have indices hk0 and the equation for the Q values reduces to
with only three constants of the metric tensor constants A, B, and F. If one takes two of the low Q values, then these can arbitrarily be assigned as Qh00 and Q0k0, giving the equations:
Combining these with the initial equation, the following equation is obtained:
In order to find zone planes, the program permutes, say, 3 low Q values with, say, the next 6 lowest Q values with h,k = ±1 or ±2, and stores calculated values of F. Values that occur frequently are stored as likely values for this variable. Hence this method of indexing should not be thought of as exhaustive: it simply works on the most frequently-occurring solutions.
Once a set of possible zone planes has been found, the next step is to combine the possible zone planes together. Arbitrarily, one of the zone planes can be considered as hk0 with parameters A, B and F, while the second one can be treated as hl0 with parameters A, C, and E. Hence the only unknown parameter is D, where
D is again found by permutations using different values for Qhkl, and the most likely solutions are again kept.
Although the method is clearly not exhaustive, it is very quick since only 3 defining parameters are required for each zone, and only low values are needed in practice for h and k. Also, it has the advantage that it is less sensitive to impurity reflections in the powder pattern than many other methods.
In order to demonstrate the zone-indexing method, some laboratory data of a chloro-organic sodium salt is shown below, plotted is Q space:
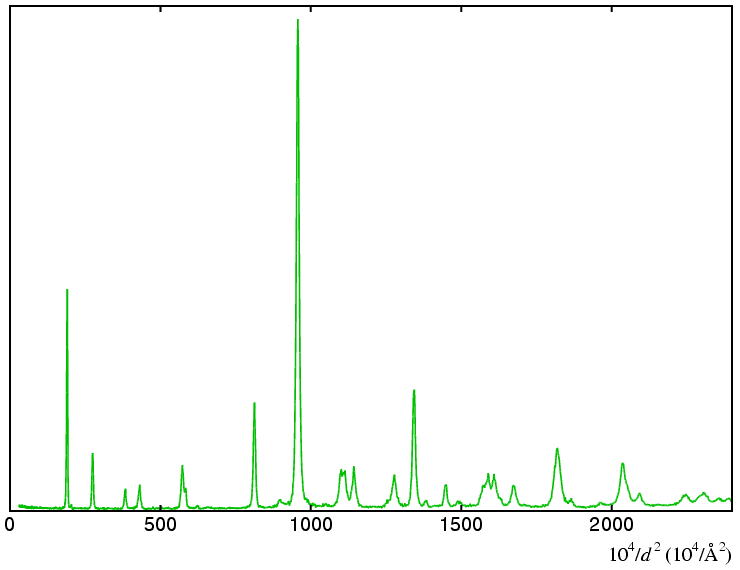
The next diagram shows the position of 20 strong and well-defined
reflections that will be chosen for indexing:

![]() ,
can be run by clicking on the icon here and submitting the form contents without
alteration. The program is preset to return only the 10 best solutions, and
sometimes the same solution may occur more than once in the list. Only consider
solutions with reasonable figures of merit, and ones that index most of the
lines. Sometimes the true solution may not index all the lines, either because
one of the lines corresponds to an impurity peak, or because of the
position of the observed lies outside the window of the position of the
calculated one.
,
can be run by clicking on the icon here and submitting the form contents without
alteration. The program is preset to return only the 10 best solutions, and
sometimes the same solution may occur more than once in the list. Only consider
solutions with reasonable figures of merit, and ones that index most of the
lines. Sometimes the true solution may not index all the lines, either because
one of the lines corresponds to an impurity peak, or because of the
position of the observed lies outside the window of the position of the
calculated one.
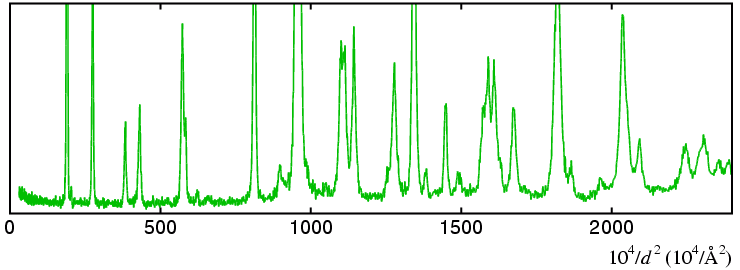
The best way to check the solutions is to generate the complete list of
reflections for the likely unit cells and compare them to the
observed data. The result, plotted again in Q space, is shown
in the red and cyan line diagram, which should be compared to
the data, now shown in expanded format below:
A complete list of reflections corresponding to the above
can be obtained by clicking on the icon for

![]() generation.
You can compare this list to the list of
2θ values used as input to the indexing program.
generation.
You can compare this list to the list of
2θ values used as input to the indexing program.
![]() Course Material Index
Course Material Index
![]() Section Index
Section Index
![]() Previous Page
Previous Page
![]() Next Page
Next Page
| © Copyright 1997-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |