Logo Reflection Conditions & Systematic Absences
Course Material Index  Section Index  Previous Page Next Page

Reflection Conditions & Systematic Absences

Consider the space group P21, which is primitive monoclinic with the symmetry operators x,y,z and -x,1/2+y,-z.

A single-crystal diffraction experiment for a crystal with this symmetry might yield data as shown below for the reciprocal lattice plane hk0:

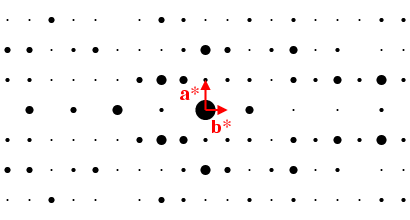
2(1)-axis

Inspection of the above figure shows that several positions in reciprocal space are characterized by zero-intensity spots. Two types of zero intensity reflections are present: some spots are exactly zero intensity due to symmetry while the others are zero intensity within experimental error. The two types are picked out in the diagram below with green and magenta circles, respectively:

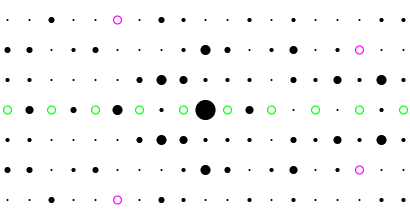
2(1)-axis

The zero-intensity spots shown in magenta occur randomly and should not be confused with the systematically-absent spots picked out in green. It is the latter line of spots that indicate that a two-one axis is likely to be present in the crystal along the b direction. (There is additional symmetry in the pattern that could indicate the presence of a symmetry axis of order two along b, though the hk0 plane alone is insufficient proof of it. Since this type of symmetry cannot be observed by powder diffraction methods, it will not be discussed in detail here.)

The points ringed in green lie along the line 0k0 with coordinates given by k = 2n + 1 where n is any positive or negative integer including zero. This may be written in the symbolic form:

0k0: k = 2n + 1
This is usually referred to as a systematic absence. It is a condition that applies to the class of reflections specified, which in this instance is the line 0k0. The other points on the line correspond to reflections that may be observed. These are specified according what is called a reflection condition:
0k0: k = 2n
Crystallographers generally work with reflection conditions. This may seem strange at first since the human eye clearly picks out the holes, i.e. the systematic absence, first. However, the determination of space-group symmetry involves testing whether reflection conditions are broken or not. Thus if a reflection is observed with indices 030 then one can safely deduce that a two-one axis along b cannot be present in the crystal structure: conversely, if the same reflection has zero intensity one cannot safely make the deduction that a two-one axis is present. In the above example, the reflection condition would allow one to say that the data is compatible with space group P21 in preference to, say, space group P2.

Reflection conditions for the different space groups are given both in the International Tables for Crystallography and on the Space Group CD-ROM. They are expressed for either a specific class of lattice points, e.g. those on a line such as 0k0 or in a plane such as hk0, or for all lattice points, hkl. How these reflection conditions arise, and the different types of reflection condition that can be observed, form the subject of the next few pages.

Course Material Index  Section Index  Previous Page Next Page
© Copyright 1995-2006.  Birkbeck College, University of London. Author(s): Jeremy Karl Cockcroft