 |
Molecular Geometry:
III. Torsion Angles |
 |
Molecular Geometry:
III. Torsion Angles |
Torsion Angles
In addition to bond lengths and bond angles, an important parameter in describing the conformation of many organic and bioorganic molecules is the torsion angle. Consider an arrangement of four atoms Cl(1),C(1),C(2),O(2) in heavy-atom structure of chloral, CCl3CH(OH)2, as shown in the sketch below:
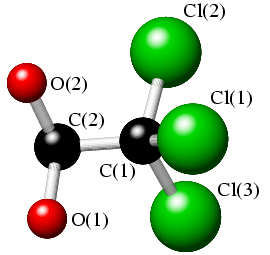
The torsion angle, χ[Cl(1),C(1),C(2),O(2)], is defined by the angle between the planes formed by atoms Cl(1),C(1),C(2) and atoms C(1),C(2),O(2) (given that any three points in space define a plane). The torsion angle, χ, which ranges from -180° to 180°, is illustrated in the two sketches below, where the view is now along the C(1)-C(2) bond (with C(2) at the back).
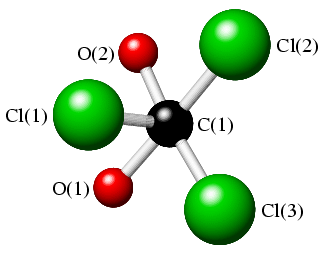 |
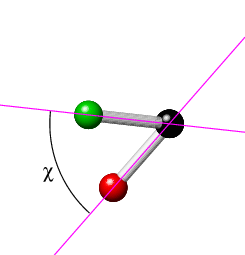 |
The torsion angle is considered positive if a clockwise rotation is required to bring atom Cl(1) into line with atom O(1). Clearly if all of the four atoms were to lie in a plane, then the torsion angle χ is 0° or 180°, depending on whether the first and fourth atoms are in a cis or trans relationship with respect to the middle bond, respectively. Simple examples of these are exhibited by the two isomers of 1,2-dichloroethene, CHCl=CHCl, in which the two chlorine atoms can be cis (see earlier figure) or trans (see earlier figure for CHBr=CHBr) to each other with torsion angles of 0° and 180°, respectively. In this particular case, the torsion angles are fixed by the C=C double bond. If the double bond is hydrogenated to form 1,2-dichloroethane, CH2ClCH2Cl, then rotation about the C-C bond becomes possible. The lowest energy conformation of the molecule is with the torsion angle Cl-C-C-Cl equal to 180°.
In contrast to the calculation of bond angles and bond lengths, where the values are frequently obtained directly from the fractional cell coordinates together with the real-space cell metric tensor, torsion angles are usually calculated using orthogonalised Cartesian coordinates. The calculation involves use of both vector dot and cross products, and a full description of the method of calculation lies outside the scope of this course. In addition to evaluating the magnitude of the torsion angle, it is also necessary to evaluate the sign. In practice, very few Rietveld programs seem to provide an option for the calculation of χ.
| © Copyright 1997-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |