Constraints & Restraints I. Coordinate

Course Material Index  Section Index  Previous Page  Next Page

Coordinate Constraints

Probably the most important constraint in crystallography is that imposed by symmetry, and a space group is invariably specified as an essential part of the description of a crystal structure. All space groups with pure rotation axes or rotary-inversion axes (including mirror planes) possess special positions (as discussed in an earlier section).

To emphasise this point, we will consider one of the two crystallographic distinct molecules in the low temperature structure of SF₆:

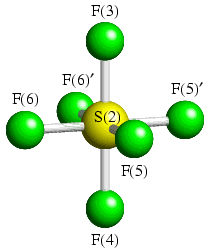
In the crystal structure, this molecule has a mirror plane (x,0,z) passing through F(3), S(2), and F(4), and bisecting F(5) and F(5)′, and F(6) and F(6)′. The following coordinate constraints are therefore applied:

• F(5)′ and F(6)′ are omitted, and the site occupation numbers for F(5) and F(6) are doubled to compensate;
• The y coordinates of F(3), S(2), and F(4) are all constrained to be zero, and are not refined.

Most modern Rietveld programs are now coded so as to constrain the atomic coordinates automatically for any of the various site symmetries that will be encountered in crystal structure refinement. When these constraints are not enforced corectly, the least-squares procedure generally leads to singular matrices or strongly diverging refinements.

An additional type of coordinate constraint that may be encountered is that used for hydrogen atoms in the refinement of organic structures, especially from X-ray data. Apart from terminal methyl groups, -CH₃, the coordinates of many hydrogen atoms can be determined assuming that the carbon atoms in the organic structure have a particular orbital hybridization, e.g. tetrahedral sp³ or planar sp² geometry. Under these conditions, it is quite common for the hydrogen atoms to be simply added to the structure and their coordinates not refined. Instead, the coordinates of the bonding atom are refined and the position of the hydrogen then adjusted at the end of each step of the refinement. This is sometimes referred to as a "riding" model for the H atoms. This constraint is standard in single-crystal refinement packages, but is less commonly available in modern Rietveld programs.

Course Material Index  Section Index  Previous Page  Next Page