Combined Data Sets

Course Material Index  Section Index  Previous Page 

Combined Data Sets

There are occasions when a single powder diffraction pattern contains insufficient information for a structure to be solved or refined. When this occurs, the use of two (or more) data sets can be very useful. In order to increase the information content available from powder diffraction, data sets can be collected using different types of radiation, for example, using both neutrons and X-rays, or with two different wavelengths, for example, by exploiting the tunable nature of synchrotron X-rays.

The diffraction patterns below, obtained on a sample of sodium methyl, NaCD₃ provide a convenient demonstration of refinement from two data sets simultaneously.

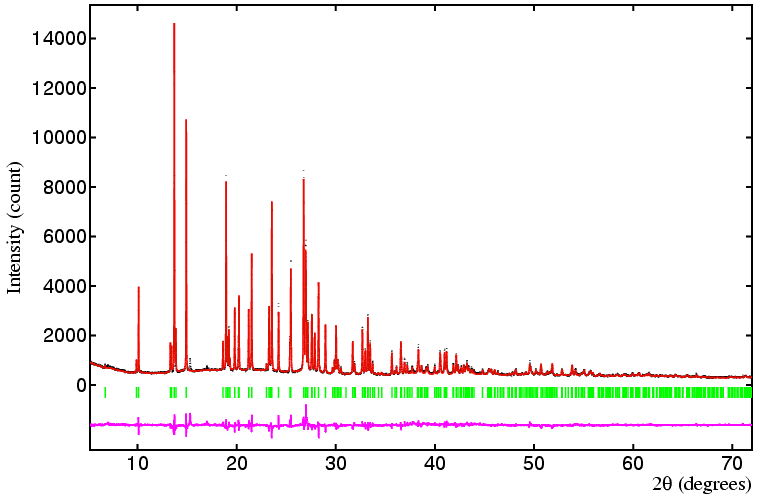
The Rietveld fit to the diffraction pattern shown above is based on X-ray data collected with λ = 1.0967 Å on instrument 9.1 at the Daresbury SRS. Contrast this with the diffraction data shown below, which is of neutron data collected with λ = 1.594 Å on instrument D2B at the ILL, Grenoble.

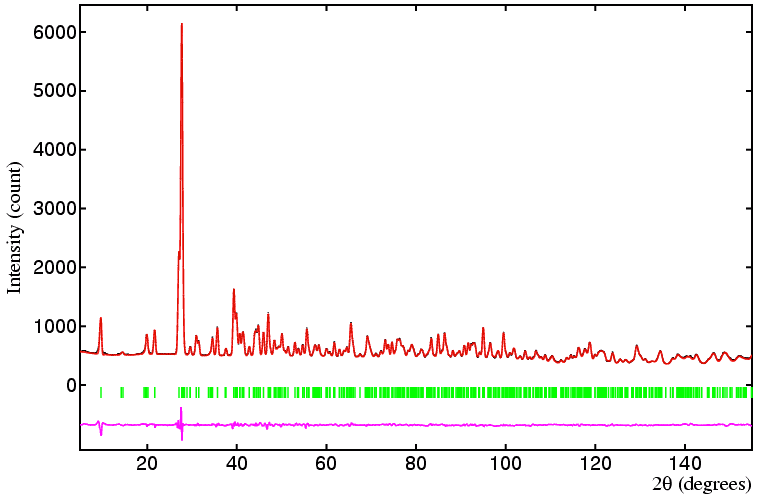
For sodium methyl, the heavy-atom structure was solved from the X-ray powder diffraction data to give the coordinates of the Na and C atoms. The neutron data were then used to locate the D atoms and refine the structure. You might then ask the question: can both data sets could be used simultaneously in the least-squares procedure so as to give better parameters?

The answer is both yes and no! With modern versions of the Rietveld program the concept of y(obs) has been extended to include two (or more) data sets as experimental observations. As with the restraints discussed earlier, it is necessary to have a weighting factor for each data set. The minimised quantity Δ (using two data sets) may then be written as:

where W_k is a weight factor assigned to each phase. Setting either weight to zero is equivalent Rietveld refinement of a structure with a single data set.

The data sets above are very dissimilar due to the different scattering lengths of the atoms for X-rays and neutrons, and precisely because of this each contributes useful diffraction information for the refinement of the crystal structure. In a combined data set Rietveld refinement, the obvious approach is to refine a single set of atomic coordinates with respect to both data sets. You may now ask: What about, say, the cell parameters? The cell parameters can be tied for each data set, but it is then important to refine to refine one the wavelength used to collect one of the data sets.

A perhaps more difficult question concerns whether the temperature factors can be constrained to be the same. If the data sets are not obtained at the same temperature, then the temperature factors will be obviously be different with respect to each data set. Hence the "no" answer to the question raised earlier. The data sets above were collected on the same sample, but at room temperature and liquid helium temperature, respectively.

In the example above, the data sets were collected on different instruments so there will an independent set of instrumental parameters (e.g. UVW) associated with each. However, even for the case of data sets collected on the same instrument, but with different wavelengths, it is still advisable to use more than one set of instrumental parameters.

Under what circumstances is it justified to use a combined data set for the refinement of the crystal structure? This is a difficult question to answer. As will be discussed later, it may be useful to collect one data set for structure solution and another for structure refinement. However, there is one case when a combined data set approach is essential. The refinement of site occupancy for two atom types distributed over two crystallographic sites is possible using a single data set: when more than two atoms are disordered over two (or more) crystallographic sites, then a single data set never contains sufficient information, and two or more data sets are essential to resolve this refinement problem.

Course Material Index  Section Index  Previous Page