Laue versus Monochromatic Methods

Course Material Index  Section Index  Previous Page  Next Page 

Laue versus Monochromatic Methods

Most of the discussion so far has implied just one kind of operation in a diffraction experiment. In fact there are two types of basic operation and we need to clarify these. By far the more popular method has been the monochromatic method though, historically speaking, the Laue method was the first to be used in 1912 (see: In the Beginning). We can distinguish between these two methods using Bragg's Law and the two diagrams below:

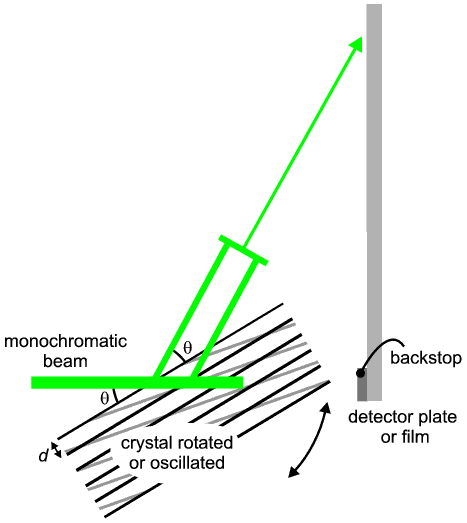
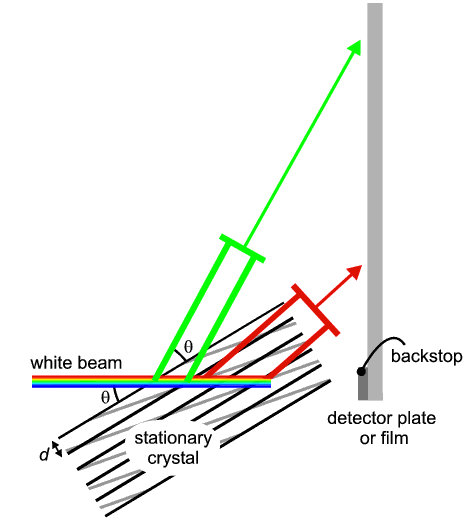
As remarked earlier, diffraction is an event which occurs when Bragg's Law is fulfilled. There are three principal parameters in Bragg's Law: λ, d, and θ (let us say, for argument, n=1). So the obvious approach is to arrange that two of these parameters remain fixed while the third parameter is varied until the equation becomes satisfied (i.e. the left hand side equals the right hand side). There are two basic ways of doing this:

Monochromatic mode

This is illustrated in the first diagram (above). The two fixed parameters are λ and d, while the third parameter, θ is varied by rotating the crystal. λ is fixed by virtue of using monochromatic radiation (for a little more detail on the meaning of monochromatic radiation, click here). Let us imagine that we select a set of crystal planes, h,k,l, with spacing d_hkl, so d then becomes the second fixed parameter which we treat as an unknown. As the crystal rotates the planes rotate with it and θ, the angle between the incident beam and these planes, changes until Bragg's Law is satisfied. When the equation is satisfied we get diffraction; when we get diffraction we can determine the value of d since it is then the only unknown in Bragg's Law. This mode is sometimes referred to as the angle-scanning mode.

Laue mode

This is a little more difficult to understand, and is illustrated in the second diagram (above). In this mode the two fixed parameters are d_hkl and θ, the crystal being fixed (i.e. it does not rotate); the continuously varied parameter becomes in effect the X-ray wavelength, λ. Let us imagine that we are interested in a given set of planes, h,k,l, as illustrated (black). Whatever orientation the crystal happens to be lying in will determine θ, the angle between the h,k, l-planes and the incident radiation. However with the Laue mode, the radiation used is not monochromatic but rather contains a full spectrum of many wavelengths (i.e. white X-rays). All these X-rays will have the opportunity to be diffracted by these black planes, but only those with a value of λ satisfying Bragg's Law will actually diffract (in this illustration the green wavelength results from diffraction off the black planes); so in effect the crystal planes select out the appropriate X-ray wavelength for diffraction (the remaining wavelengths are scattered in a non-intense fashion contributing to the background and straight through beam). However what complicates the issue is that simultaneously there will be many other planes (e.g. grey as illustrated) also receiving this white radiation, each with their individual (different) θ-angles. Therefore for each combination of planes plus θ, there will be a wavelength value that satisfies Bragg's Law. So simultaneously each set of planes will be selecting out those X-ray wavelengths that can diffract, each at different wavelengths and each in a different direction (note that a different θ implies a different diffracted direction). Thus the net result from a Laue exposure is usually a mass of diffraction spots on the photographic film, each spot corresponding to a different diffracting plane and a different wavelength. Sorting these out can be a considerable problem requiring computerised indexing and prediction.

Course Material Index  Section Index  Previous Page  Next Page