Variations Across a Pattern

Course Material Index  Section Index  Previous Page  Next Page 

Variations Across a Pattern

In the above we have discussed peak shape, and its representation by different functions, as though we were referring to just one particular peak in a powder diffraction pattern. In practice it is more often the case that we will want to group together a number of peaks within a pattern for our attention. A common assumption used is that if one collects a complete powder diffraction pattern then the inherent shape of different peaks across the pattern will be essentially the same for a given single component sample on a given diffractometer system. This assumption appears to work well in the field of Rietveld structure refinement (which will be covered later in the course) where one usually assumes that across a pattern only three peak parameters vary:

• the peak position, 2θ₀ 
• the total peak intensity, I₀ 
• the peak width, B (i.e. H or β)

In Rietveld refinement one normally fits the same peak-shape function to every peak in the pattern to determine 2θ₀ , I_tot and B individually for each peak. This is illustrated below for the same two peaks of yttria discussed earlier in this section: you can click on the two boxed peaks to see the detailed fitting and differences obtained using a pseudo-Voigt function.

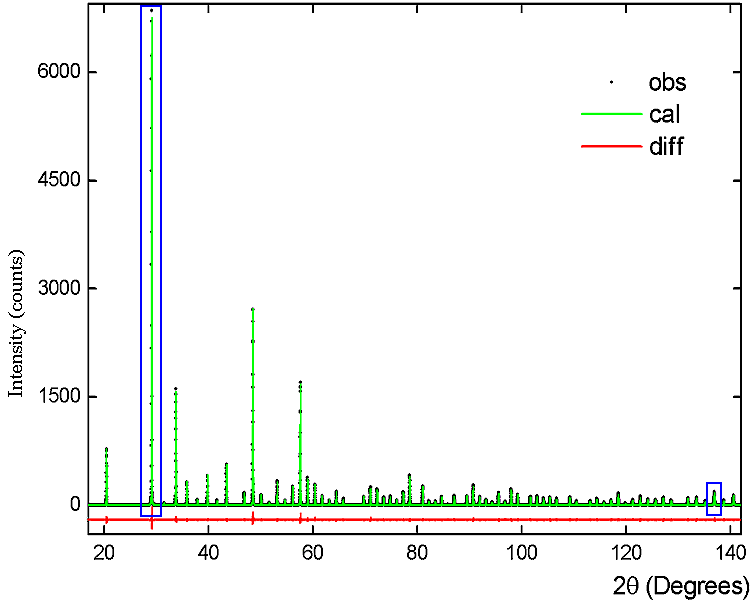
However life is rarely so simple and often in practice many peaks will be overlapped preventing such individual treatment. In such cases it is desirable to be able to define a basic peak shape and attribute it to all the peaks, overlapped or otherwise, but making allowance for their different positions in 2θ. The question arises then as to how the peak width, B, varies from peak to peak across the whole pattern. As a result of the much-quoted study of instrumental broadening of neutron diffraction peaks (G.Cagliotti, A.Paoletti and F.P.Ricci, Nucl. Instrum. Methods 35, 223-8 (1958)) and many subsequent confirmations since for X-ray diffraction, it is now more or less universally accepted that the following formula:

may be used in structure refinement applications, but not in certain cases of anisotropic peak broadening or non-standard angular situations.

So one strategy adopted when U, V, W are unknown is to determine 2θ₀ , I₀ and B from a reference material, either by whole-pattern fitting or by individual peak fitting, then solve/fit for the three unknowns U, V, W (so as long as there are 3 or more resolved peaks there will be a solution). The above formula is then used to calculate a width of any unresolved peaks.

Course Material Index  Section Index  Previous Page  Next Page