Sources of Peak Broadening

Course Material Index  Section Index  Previous Page  Next Page 

Sources of Peak Broadening

We address the question of what causes peak broadening, resulting in the peak shapes we have just discussed. If we had a perfect sample and a perfect diffractometer the diffraction peaks would be extremely sharp (peak widths as narrow as seconds of arc). In practice such perfection is not realised and typically good powder diffraction patterns display peaks with widths that are measured in hundredths of degrees. This broadening arises from two sources:

(a) Instrumental Contributions
(b) Sample Contributions

Before we discuss these contributions in more detail it is necessary to first familiarise ourselves with the idea of convolution as it applies to this situation. We have here two effects: broadening from an imperfect diffractometer ("instrument") and broadening from an imperfect sample. These effects are inter-dependent in the sense that any imperfection in one (e.g. just one imperfect powder crystallite) will in turn be subject, statistically, to all the imperfections of the other (the instrument), and then the same applies to the next crystallite and so on. So to determine the final result we have to sum every combination of the imperfections of one factor acting upon all the imperfections of the other factor. This type of situation is known mathematically as a convolution and is expressed by an equation that might look like:

where ψ plays the part of a dummy variable covering the full range of possibilities. However the important point of all of this seemingly "side issue" is to realise that the effects of convolution are not always intuitively obvious. Some functions convolute in a simple way: For example two Gaussian functions convoluted with each other produce another Gaussian function in which the final width follows a simple square law:

Gaussian:

whereas two Lorentzians convoluted would yield a width equal to just the sum:

Lorentzian:

Other functions may convolute in more complex fashion to the point that the final function is unrecognisable from the original two functions. De-convolution (the reverse procedure in which one recreates one of the original two functions from the convoluted result and a knowledge of the other original function) is equally non-obvious and in some cases is impossible. The take home lesson from all of this is that determining, say B_sample, from the measured broadening, B_total, is not necessarily simple. However there are many research situations where a highly rigorous and accurate value is not required and an approximate value would suffice. In some situations it may, for example, be acceptable to assume either the Gaussian or Lorentzian cases given above.

Returning then to the two sources of broadening:

A. The Instrumental Contribution.

This arises from factors such as the following:

1. the source of radiation (X-rays or neutrons) has a finite physical size (i.e. is not a perfectly sharp spot or line)
2. the radiation is not perfectly monochromatic, but rather consists of a small range, δλ, of wavelengths around the mean, λ
3. the active diffracting volume within the sample is finite and therefore diffraction occurs away from the true centre of the diffractometer - this factor can be compounded by a low sample absorption to the radiation
4. axial divergence of the incident/diffracted beams
5. the configuration of defining slits used in the diffractometer
6. any misalignment of the diffractometer

These effects are illustrated symbolically below:

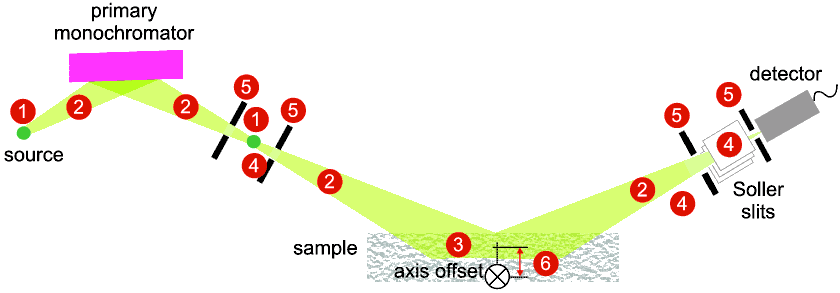
The usual way to measure the Instrumental broadening contribution of a diffractometer is to use a near-perfect sample whose broadening contribution is negligible in comparison. Suitable materials for this purpose include LaB₆, BaF₂ and KCl.

B. The Sample Contribution.

This arises from factors (T.Ungar in "Industrial Applications of X-ray Diffraction" eds: Chung & Smith, Marcel Dekker, New York, @2000, page 847) such as:

• crystallite/diffracting domain size
• crystal lattice distortion (micro-strain) due to dislocations and concentration gradients
• structural "mistakes" such as stacking faults, twin faults or layer mistakes
• concentration gradients in non-stoichiometric compounds

More rigorous methods are mentioned later. The usefulness of B_sample is discussed next.

Course Material Index  Section Index  Previous Page  Next Page