Logo Properties of the Neutron
Course Material Index  Section Index  Previous Page  Next Page 

Properties of the Neutron

The neutron is a particle with a spin of one-half. It is the interaction of this spin with the spin state of the nucleus of an atom that determines the scattering property of a neutron with that atom. This spin-spin interaction leads both to coherent scattering, and hence diffraction effects, and to incoherent scattering, which for the purposes of powder neutron diffraction ends up as general background noise in the data. A neutron may also simply be absorbed by the nucleus of an atom, a property that is made use of in the detection of neutrons. Finally, though it goes beyond the scope of this course, the spin of the neutron may interact with the spin of any unpaired electrons of an atoms, which leads to so-called magnetic scattering. The following paragraphs describe these interactions in more detail.

Scattering length b

For the case of X-ray diffraction, the intensity of a reflection, Ihkl, is proportional to the square of its structure factor, Fhkl. As shown in the section on diffraction theory, the latter is given by the equation

  N 
Fhkl =  Σ   fn exp{2πi (hx + ky + lz)} exp{-Wn}
  n=1 

where fn is the scattering factor for atom n within the unit cell. For neutron diffraction, the structure factor is given by a similar expression with the single exception that the X-ray scattering factor, f, is replaced by the neutron scattering length, b. The X-ray scattering factor, f, of an atom is quite different to the neutron scattering factor, b, of the same atom. The reason is that X-ray diffraction results from scattering by the electrons of an atom while neutron (non-magnetic) diffraction is due to scattering from the nucleus of an atom. This has two consequences:

Firstly, the atomic nucleus acts a pin-point scatterer unlike the electron cloud, which is of finite size compared to the wavelengths used. The implication of this is that b is independent of the scattering angle, 2θ, in contrast to the X-ray case where f has a form factor that decreases with increasing scattering angle. Thus the smaller d spacing information is relatively better determined in a neutron experiment compared to a similar X-ray experiment. This results in more precise atomic thermal parameters being determined from powder neutron data.

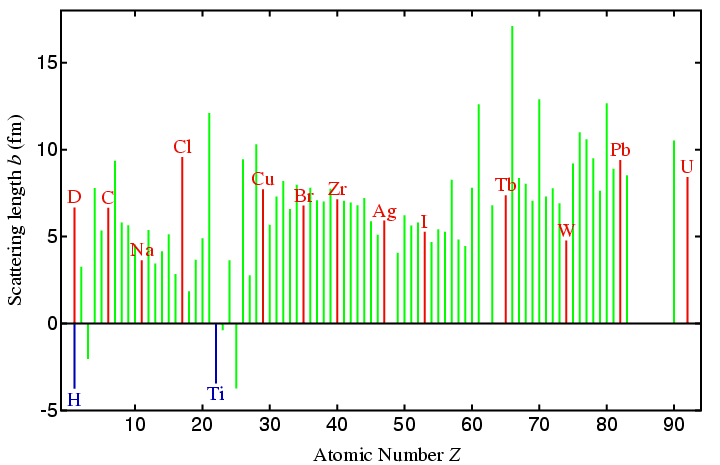
Secondly, for X-rays, f at zero scattering angle, is simply equal to the number of electrons in the atom (or ion), i.e. f (2θ) = Z for 2θ = 0°. By contrast, the neutron b values are a property of the nucleus and do not vary in the systematic way that the equivalent f values do in the X-ray case. The figure below shows the variation of b value as a function of atomic number. The most convenient units for the scattering length values is fm (= 10-15 m).

The table that follows lists values for the neutron scattering lengths of a few atoms together with their atomic number to allow a simple comparison with the X-ray case. (A direct comparison can be made by multiplying f (0°) value by the classical electron radius, re, equal to 2.818 fm. However, X-ray scattering lengths are rarely used in practice since the proportionality constant re is best ignored for most practical purposes.)

Element H D U Fe Co Ba O V Ti Zr
X-ray f (0°) (Z) 1 1 92 26 27 56 8 23 22 40
Neutron b (fm) -3.740 6.674 8.420 9.450 2.780 5.280 5.805 -0.3824 -3.438 5.280
From the table, you should note that isotopes of a given element have different neutron scattering lengths. For most neutron powder diffraction studies this is not important, though it has been very important in the study of liquids. The important example to be aware of here is the case of hydrogen and its isotope deuterium: their scattering lengths differ in both magnitude and sign. By mixing the isotopes in a ratio that it is inversely proportional to their scattering length, it is possible to achieve a net scattering length of zero. This fact has been much exploited in neutron small-angle scattering, but is less relevant to powder neutron diffraction. However, the different scattering properties of hydrogen and deuterium atoms are relevant to powder diffraction and will be discussed further below.

You should note that "heavy" elements do not scatter on average very much more than lighter ones (compare D and U in the table). In addition, adjacent elements that would be difficult to distinguish in a laboratory X-ray experiment may scatter very differently, a well-know example being that of Fe and Co (as given in the table). Historically, much powder diffraction research with neutrons has been on oxide systems: a comparison of, say, Ba with O in the above table shows the scattering power of these elements is similar in stark contrast to the X-ray case.

A few elements scatter neutrons very weakly, a notable example of this being vanadium, which has a tiny negative scattering length. This property is exploited in the manufacture of sample holders for powder neutron diffraction (see later page). Finally, for some medium high-pressure studies a metal titanium-zirconium (68%:32%, b = 0.0 fm) alloy has been used, which exploits the fact that titanium is one of the few metals with a large negative scattering length.

Absorption cross-section σabs

A consideration of neutron scattering lengths if not the only factor that should be taken into account when contemplating a powder neutron diffraction experiment. For the X-ray case, the scattering and absorption of X-rays both increase with increasing atomic number Z, though with absorption it may suddenly change due to absorption edges (as shown in the section on X-ray filters). Neutrons have the desirable property that they are only absorbed by a few nuclei as shown on the figure below:


Although the figure shows absorption as a function of atomic number, strictly speaking it is actually a function of isotope. Thus, although lithium has a relatively high absorption cross-section for neutrons, it is only the 6Li, which is present in naturally-occurring samples at approximately 7.5%, that is a very strong absorber of neutrons: the absorption cross-section of 7Li, which is the main isotope of Li, is about 20000× smaller than that of 6Li. The absorption of neutrons by certain isotopes is exploited in the design of detectors for neutron diffractometers. From the above figure you should observe that powder neutron diffraction experiments are going to be very difficult (if not impossible) for compounds containing certain elements, especially for many of the rare-earth elements (such as Gd, Sm, Eu, and Dy).

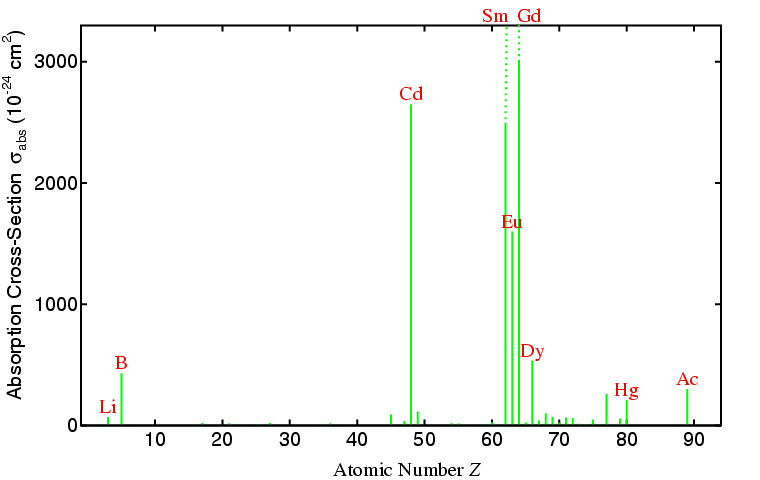
You can see from the above figure that neutron cross-sections (for absorption and scattering) are very small numbers when quoted in cm2. They are often given in a more convenient unit called a barn, where 1 barn = 10-24 cm2.

Incoherent cross-section σinc

It was mentioned that the spin-spin interaction of the neutron with the nucleus of an atom leads to both coherent and incoherent scattering. How this arises need not concern us. However, you should be aware that a few isotopes have very large cross-sections for incoherent scattering as shown in the following figure:


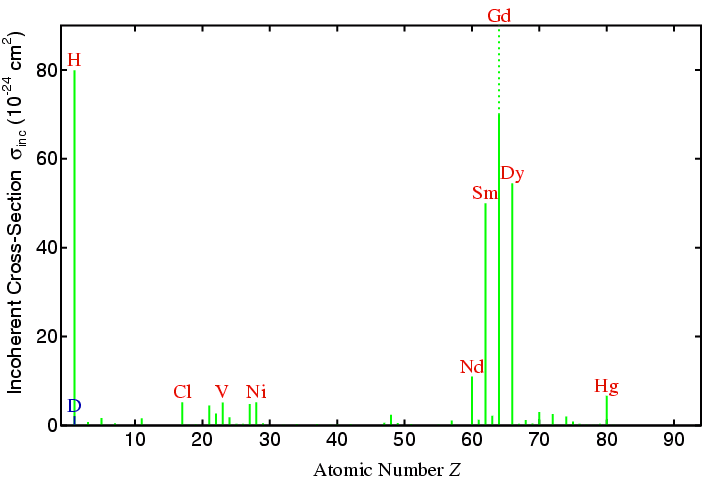
From the figure, you can see that hydrogen (isotope 1H) scatters very incoherently in contrast to deuterium (isotope 2D). The implications of this in the preparation of samples for powder neutron diffraction is discussed subsequently.

Temperature of the neutron

The kinetic energy, E, of the neutron is given by mv2/ 2, which is conventionally related to temperature via the Boltzmann constant, kB (= 1.381×10-23 JK-1), according to the equation:

E = mv2 / 2 = kBT

Taking room temperature as 20°C, i.e. 293 K, a velocity equal to 2200 ms-1 is obtained for thermal neutrons, which therefore have a wavelength that is approximately equal to 1.8 Å. You may note that many scattering properties of the neutron are quoted for this specific wavelength, velocity, and energy. Neutrons with long wavelengths are often referred to as cold neutrons, while at the other end of the scale, those with short wavelengths are usually known as hot neutrons.

Polarisation

Although neutrons can be polarised in terms of their spin, this property is only important for single-crystal magnetic experiments. For neutron powder diffraction, there is no polarisation factor in contrast to the equivalent the X-ray case.

Generation of neutrons

Intense neutron beams cannot be produced in the laboratory. Currently, there are two methods for producing neutron beams of sufficient intensity for powder diffraction work, namely, a nuclear reactor and a pulsed source. The two methods are quite different and result in neutron beams with different characteristics. Both methods involve fission, though with a pulsed source it is not necessary to use a naturally fissile material. The consequences of the two methods in terms of the design and function of neutron powder diffractometers will be discussed separately in later pages of this section of the course.

Course Material Index  Section Index  Previous Page  Next Page 
© Copyright 1997-2006.  Birkbeck College, University of London. Author(s): Jeremy Karl Cockcroft