 |
Accuracy |
 |
Accuracy |
Accuracy
So far only the precision of our refined cell parameters has been discussed. While precise parameters are desirable, it is usually important that the values are also accurate. In order to demonstrate some points concerning accuracy, it is convenient to use powder diffraction data collected on a well-annealed yttria sample as shown below:
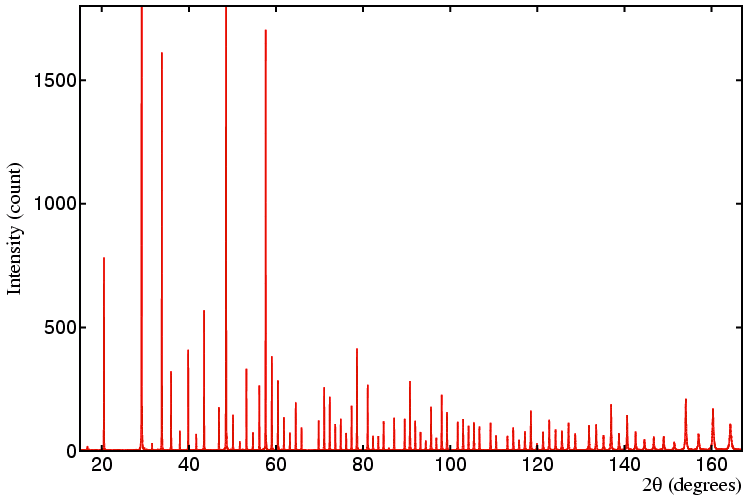
Yttria is used since its cubic symmetry and relatively large lattice parameter result in a large number of well-separated peaks that extend out to the maximum scattering angle permitted by the diffractometer software. As for the silicon data shown earlier, the data were collected using a flat-plate sample in Bragg-Brentano reflection geometry. For demonstration purposes, three different data sets were collected, which will be referred to as A, B, and C.
Try the three unit-cell refinements below and note the results:
You should see that the lattice parameter refines within the precision
of the results to approximately 10.602 Å in each case, but that the
2θzero error varies in each case.
One of the data sets corresponds to a well-aligned instrument, while the
other two patently do not. It is important to realize that all three
refinements produce an accurate result within the precision determined
by the esd's despite the fact that the
2θzero error correction is being misused;
the latter is actually compensating for errors due to sample height displacment
effects.
Now repeat the exercise, but edit the form so that the
2θzero error is not refined.
This time you will observe large variations in the refined value of the cubic
cell parameter a: in two cases the value obtained
will be very inaccurate, though this is not evident
from the cell parameter esd'd obtained from the refinement.
The previous exercise involved the low-angle data. Now observe the effects
when only the high-angle data is used for the refinement of the cell parameter
with the zero correction omitted:
For the two data sets where the sample height is incorrect, the accuracy
of the value of a is much improved by using the high-angle data only
for the refinement. You should be able to see in the list of the
differences between observed and calculated angles that the error due
the sample height displacement effect is still present, but that its
effect is much reduced. You may like to try the same refinements again, but
with 2θzero allowed to refine.
Although accuracy of the unit-cell parameters is clearly effected
by instrumental effects such as sample displacement and instrument
misalignment, it can also be affected by other factors such as
sample purity, transparency, or even absorption: different samples may
have slightly different lattice parameters; hence the need for standard
samples as described earlier. Refinement of the lattice parameters
of organic compounds is likely to result in inaccurate values when deep
flat-plate sample holders are used; also small peak shifts may occur
in transmission geometry for samples which absorb heavily, so beware
of potential inaccuracies under these conditions too.
![]() Unit-cell refinement using high-angle
2θ values from data set A.
Unit-cell refinement using high-angle
2θ values from data set A.
![]() Unit-cell refinement using high-angle
2θ values from data set B.
Unit-cell refinement using high-angle
2θ values from data set B.
![]() Unit-cell refinement using high-angle
2θ values from data set C.
Unit-cell refinement using high-angle
2θ values from data set C.
![]() Course Material Index
Course Material Index
![]() Section Index
Section Index
![]() Previous Page
Previous Page
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Jeremy Karl Cockcroft Martin Vickers |