Rotational Symmetry: Symmetry Operators

Rotational Symmetry

II. Symmetry Operators

Course Material Index

Section Index

Symmetry Operators

Given the atomic coordinates of a molecule in a crystal structure, it is often necessary to know the coordinates of the atoms of symmetry-related molecules. In order to do this, it is necessary to know how the (x,y,z) coordinates of the atoms in the first molecule relate to the atoms in the second. Symmetry operators can transform the coordinates of one molecule to those of another. This section explains the form of these symmetry operators for pure rotational symmetry.

Consider a twofold rotation axis parallel to the Z-direction (of a right-handed conventional Cartesian system of axes) and passing through the point (0,0,0), i.e. the origin, and an atom with coordinates (x,y,z) as shown below:

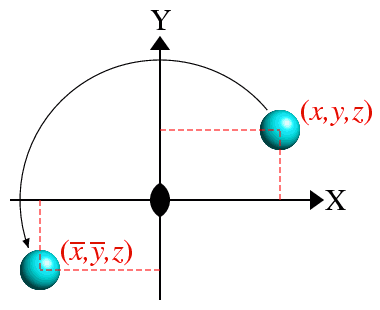
Notice that the twofold axis is represented in the figure by a lens-shaped symbol at the origin. Applying a 180° rotation about the axis to the atom in the top-right of the diagram brings it to the position at bottom-left as shown. The x- and y-coordinates of the symmetry-related atom are simply the negative values of the atom's coordinates before the symmetry operation was applied, while the z-coordinate of the atom remains unchanged. Note that in the figure, the negative value is indicated by a minus sign "-" which is put above the "x" and "y" in common with standard crystallographic convention. Thus the symmetry operator for a twofold axis passing through the origin is simply (-x,-y,z).

The symmetry operator for a twofold rotation through the origin may seem a little obvious. If so, what is the symmetry operator for a twofold rotation about the Y axis?

Consider now the case of a fourfold rotation axis about the Z axis as shown below:

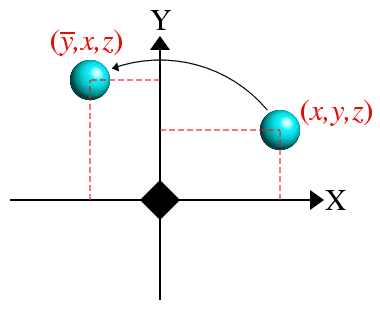
You should now notice that the fourfold axis is represented by a square-shaped symbol at the origin. (A full table of these symbols will be found at the end of this first section on symmetry.) Applying a 90° rotation about the axis to the atom in the upper-right of the diagram brings it to the position at top-left as shown above. The operation of rotation leaves the z-coordinate of the atom unchanged as before. The transformed atom has coordinate values that are negative for x and positive for y, but this does not imply that the symmetry operator is -x,y,z. Quite the opposite!

To see this consider an atom with coordinates (2,1,5) that rotates to the position (-1,2,5) under the action of the fourfold rotation. The new x-coordinate value (-1) is equal to the negative of the untransformed y coordinate value (+1), while the new y-coordinate value (+2) is equal to the positive value of the untransformed x coordinate (+2). Thus the symmetry operator for a positive fourfold rotation about the Z axis is not -x,y,z, but -y,x,z.

What is the symmetry operator for a negative fourfold rotation about the Z axis?

The next figure shows the operation of threefold symmetry on an atom. You will immediately observe that the coordinate system is no longer Cartesian. For threefold (and also sixfold) symmetry, crystallographers usually choose a set of axes so that the angle between the X and Y directions is 120° (= 360°/3), with the Z direction perpendicular to both X and Y. What is the reason for this?

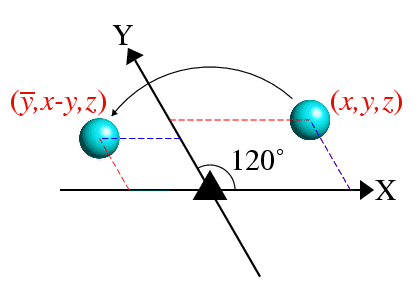
The answer is the simplicity of the symmetry operators for threefold and sixfold rotations with this system of coordinates. With this non-orthogonal axis system, the symmetry operator for a positive threefold rotation about the Z axis is given by (-y,x-y,z). That this is correct can be seen by inspection of the dashed lines in the figure where the blue ones are both of equal length and the short red one is equal to the difference in length between the long red and blue lines. Compare the simplicity of this expression to the symmetry operator for a threefold rotation in a coordinate system with Cartesian axes:

( - x/2 - y√3/2, x√3/2 - y/2, z)

Using the above axis system, the expression for a positive sixfold rotation is equally simple and takes the form (x-y,x,z).

Whereas most crystallographers can readily remember (or deduce) symmetry operators for twofold and fourfold rotations, the expressions for threefold (and sixfold) are not so easy to remember. However, crystallographers are not required to remember them all since they have been extensively tabulated for different crystal systems, both in books, CD-ROM, and in most of the modern crystallographic computer software.

The above examples of symmetry operators all refer to symmetry axes that pass through the origin (0,0,0) of coordinate space. Normally this is the case for high symmetry axes. However, it is very common for twofold axes in a crystal not to pass through the origin as will be demonstrated later. The question then arises as to the form of the symmetry operator for an axis not passing through the origin as illustrated in the figure below:

The figure shows a twofold rotation axis parallel to the Z-direction whose X,Y coordinates are (T_x,T_y). When an atom at an arbitrary position (x,y,z) is rotated about this axis, what are the coordinates of the symmetry related atom? Consider first what happens to the x-coordinate. The difference in X between the initial atom position and the rotation axis is x-T_x. Likewise, by symmetry the difference in X between the atom position after rotation and the axis is x-T_x. Hence the x-coordinate of the atom after the symmetry operation is:

x - 2 × (x - T_x) = 2T_x - x

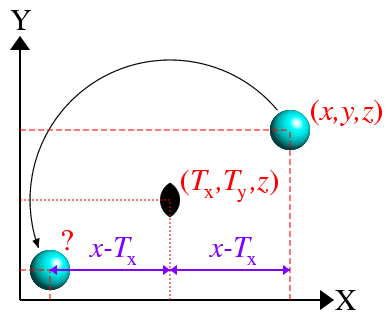
Applying a similar argument to the y-coordinate, one can show that the coordinates of the atom after the symmetry operation are (2T_x-x,2T_y-y,z) with the z-coordinate being unchanged by the symmetry operation as before. Thus the symmetry operator for a twofold rotation axis at, for example, (0,1/4,z) is -x,1/2-y,z.

What is the symmetry operator for a twofold rotation axis parallel to X and passing through the point (x,1/4,1/4)?

Finally, you may have noticed that no symmetry operators have been given for, say, a fivefold rotation axis. Although rotation axes of order, for example, 5, 7, 9, etc., do exist, they cannot exist as part of the long-range symmetry exhibited by a crystal lattice. This limits the number of types of rotation axes that crystallographers need to consider to 2, 3, 4, and 6, as will be shown in the section on translational symmetry.

Course Material Index

Section Index

Author(s): Jeremy Karl Cockcroft