Glide Symmetry

Glide Symmetry

Course Material Index

Section Index

Glide Symmetry

Concepts

The previous pages on screw axes demonstrated the advantages for molecular packing of a symmetry operator that is a combination of rotation and translation compared to that of pure rotation. A similar case can be made for the mirror planes discussed earlier. The effect of a mirror plane on the row of molecules used earlier is shown below:

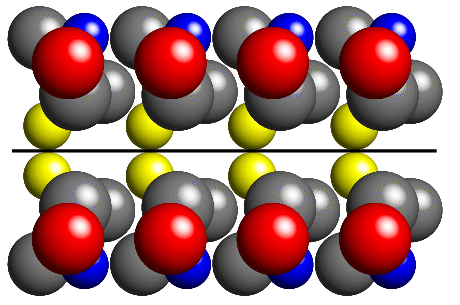
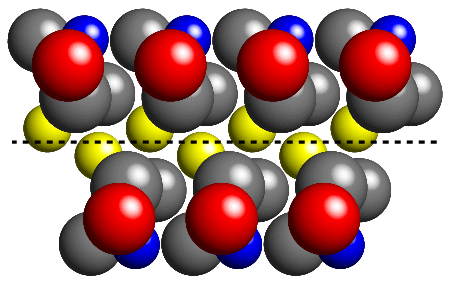
As with the case of the proper rotation axis, the figure shows that the mirror plane is bad for molecular packing. The packing is much improved by translating the row of molecules after the reflection operation as shown in the following figure:

The single operation of reflection and translation is called a glide and the symmetry element is called a glide plane. The direction of the translational is parallel to that of the plane and the magnitude is proportional to a half of the repeat distance in this instance.

Symbols, Notation, and Operators

A variety of directions are permissible for the translational component of the symmetry operator and so various symbols are required to indicate glide planes. For example, in the above example, a dashed line is used (in contrast to the solid line used for the mirror plane symmetry) to indicate that the translation is along the direction of the line itself. When the translation is perpendicular to the line, a dotted line is used, and so on. A complete list of symbols is provided in the reference page that follows this one.

The labels for this symmetry element depend on the direction (and magnitude) of the translation: the letters a, b, and c are used to indicate that the translational component of the glide plane is 1/2 a, 1/2 b, and 1/2 c, respectively. Note that these labels do not provide any information about the direction of the reflection component of the glide plane. Various other letters, such as n and d are also used for other types of glide plane: these will not be discussed in detail here.

If the glide plane in the above figure has its normal to the screen Y direction and passes through the origin, then the effect of the symmetry element is to reverse the sign of the y coordinate (due to reflection) and to add one-half to the x coordinate (due to translation). The resulting symmetry operator, in this instance, is therefore given by 1/2+x,-y,z; and the symbol for the glide plane is a.

What is the symmetry operator for a b-glide plane passing through the point (0,0,0) and whose normal is parallel to the X direction?

Course Material Index

Section Index

Author(s): Jeremy Karl Cockcroft