 |
Molecular Geometry
I. Interatomic Distances & Bond Lengths |
 |
Molecular Geometry
I. Interatomic Distances & Bond Lengths |
![]() The mathematical details given in this page are to be treated as
extra-curricular material.
The mathematical details given in this page are to be treated as
extra-curricular material.
Interatomic Distances & Bond Lengths
Calculating Distances in Real Space
In Cartesian coordinates, the distance, r, between the points P and Q is given by Pythagoras' rule as:
In vector notation, the points P and Q may be represented by the vectors
| P = XPi + YPj + ZPk | and |
| Q = XQi + YQj + ZQk | . |
The vector r between P and Q is simply the difference between them, i.e.
| r | = | P − Q |
| = | (XP − XQ) i + (YP − YQ) j + (ZP − ZQ) k | |
| = | ΔX i + ΔY j + ΔZ k |
Thus, in principle, it is relatively straightforward to calculate distances between any two points in Cartesian space. However, as a result of symmetry, crystallographers use a coordinate system with fractional coordinates based on a unit cell defined by the vectors a, b, and c. In order to calculate distances between atoms, one solution is to convert all of the fractional coordinates to Cartesian by matrix multiplication:
| ( X ) | ( a | b cosγ | c cosβ | ) ( x ) | ||
| ( Y ) | = | ( 0 | b sinγ | c (cosα − cosβ cosγ) / sinγ | ) ( y ) | |
| ( Z ) | ( 0 | 0 | 1/c* | ) ( z ) |
The disadvantage of this method is that the crystallographic symmetry operators cannot be applied readily to the Cartesian coordinates. A neater approach to the problem of distance calculation is illustrated below using some vector mathematics.
Consider again two points P and Q with fractional coordinates based on the unit cell. In vector notation these may given by the equations:
| P = xPa + yPb + zPc | and |
| Q = xQa + yQb + zQc | . |
| r | = | P − Q |
| = | (xP − xQ) a + (yP − yQ) b + (zP − zQ) c | |
| = | Δx a + Δy b + Δz c |
This is similar to the earlier equations for r, but with a, b, and c as the basis vectors. Calculating the length of the vector r from vector dot product gives:
| r2 | = | r • r |
| = | (Δx a + Δy b + Δz c) • (Δx a + Δy b + Δz c) | |
| = | Δx2 (a • a) + Δy2 (b • b) + Δz2 (c • c) + 2 Δy Δz (b • c) + 2 Δz Δx (c • a) + 2 Δx Δy (a • b) | |
| r2 | = | a2 Δx2 + b2 Δy2 + c2 Δz2 + 2bc cosα Δy Δz + 2ca cosβ Δz Δx + 2ab cosγ Δx Δy |
You should note that this key expression is very similar in format to that used for calculating d spacings in reciprocal space: the 6 terms a2, b2, ..., and bc cosγ define what is known as the real-space metric tensor.
Bond Lengths
Using the equation given in red, any distance between two points within a crystal can be calculated. With reference to the example data on sulphur hexafluoride, one can calculate the distance between S(1) and F(1) as follows: The first step is to calculate the real-space metric tensor as shown below:
| a2 = 13.80102 = 190.4676 Å2 |
| b2 = 8.14002 = 66.2596 Å2 |
| c2 = 4.74932 = 22.5559 Å2 |
| bc cosα = 8.1400 × 4.7493 × cos 90° = 0 Å2 |
| ca cosβ = 4.7493 × 13.8010 × cos 95.590° = −6.3847 Å2 |
| ab cosγ = 13.8010 × 8.1400 × cos 90° = 0 Å2 |
The next step is to calculate the distance between S(1) and F(1) in fractional coordinates:
| Δx = 0.0687 − 0 = 0.0687 |
| Δy = 0 − 0 = 0 |
| Δz = 0.2817 − 0 = 0.2817 |
Applying the formula for the square of the distance (and omitting the terms equal to zero), we obtain:
| r2 | = | 190.4676 × 0.06872 + 22.5559 × 0.28172 - 2 × 6.3847 × 0.2817 × 0.0687 Å2 |
| = | 0.8990 + 1.7899 − 0.2471 Å2 | |
| = | 2.442 Å2 | |
| → r | = | 1.563 Å |
Although this value of 1.563 Å corresponds to the distance between S(1) at (0,0,0) and F(1) at (0.0687,0,0.2817), the question that arises is does this value correspond to an S-F bond length, i.e are the atoms labelled S(1) and F(1) bonded together within the unit cell? The answer is yes! But how do we know this?
From the numerous crystal structures that have been carried out over the last 80 years, it is possible to make certain generalizations about the sizes of atoms: for ionic structures, for example, it is possible to construct a table of ionic radii as shown below (values in Å):
| Ag+ | 1.15 | Ce3+ | 1.01 | Cs+ | 1.67 | Hg2+ | 1.02 | Mn2+ | 0.83 | Pt2+ | 0.80 | Sr2+ | 1.16 | Zn2+ | 0.74 | I- | 2.20 |
| Al3+ | 0.54 | Ce4+ | 0.87 | Cu+ | 0.77 | K+ | 1.38 | Na+ | 1.02 | Pt4+ | 0.63 | Th2+ | 0.94 | NH4+ | 1.48 | O2- | 1.40 |
| Ba2+ | 1.35 | Co2+ | 0.75 | Cu2+ | 0.73 | La3+ | 1.03 | Ni2+ | 0.69 | Ra2+ | 1.43 | Ti2+ | 0.86 | Br- | 1.96 | S2- | 1.84 |
| Ca2+ | 1.00 | Co3+ | 0.61 | Fe2+ | 0.78 | Li+ | 0.76 | Pb2+ | 1.19 | Rb+ | 1.52 | Ti2+ | 0.61 | Cl- | 1.81 | Se2- | 1.98 |
| Cd2+ | 1.95 | Cr3+ | 0.62 | Fe3+ | 0.65 | Mg2+ | 0.72 | Pd2+ | 0.86 | Sn2+ | 0.93 | Tl2+ | 1.50 | F- | 1.33 | Te2- | 2.21 |
For ionic structures, one simply adds the appropriate pair of radii together in
order to obtain an approximate interionic distance,
e.g. the predicted distance for Na to Cl in NaCl will be
For organic crystal structures, where covalent bonding is the norm, there are tables of typical values for C-C distances, etc., a few of which are given in the following table (with values in Å):
| C-H | 1.07 | C-C | 1.54 | C-N | 1.47 | C-0 | 1.43 | |
| N-H | 1.00 | C=C | 1.34 | C=N | 1.32 | C=0 | 1.22 | |
| O-H | 0.96 | C≡C | 1.20 | C≡N | 1.16 | C≈C | 1.40 | (aromatic) |
Clearly, the typical covalent bond length is in the range 1 to 2 Å.
Bond Length Errors
A full description of the error calculation is beyond the scope of this course. The principles are straightforward, but the long equations are very tedious to apply by hand. Unit-cell parameters as determined by the Rietveld method are usually an order of magnitude more precise than the refined fractional atomic coordinates. However, from powder diffraction data, the esd's on the bond lengths can be determined solely from the esd's in x, y, and z. Using the sulphur hexafluoride data, the error in the value of the lattice parameter a is 2 in 138010, i.e. 0.0014%. By comparison, the error in the x coordinate of, say, F(3), is 2 in 7469, i.e. 0.027%, which is an order of magnitude larger.
Rietveld programs can calculate statistical errors in the value of the bond lengths, but these are not the only source of error. To return to the example of sulphur hexafluoride, Rietveld refinement gave a value for the S(1)-F(1) bond length of 1.563(3) Å at 5 K. When the sample was heated to 60 K, this value appeared to have decreased to 1.544(3) Å. The difference is not statistical; it is a real effect despite the fact that the actual bond length is independent of temperature (within the statistical errors of most experiments). So why the discrepancy? The two values differ because the molecule librates about the central sulphur atom as the temperature is increased. As a result, the average position of the fluorine atom appears closer to the central sulphur atom at the higher temperatures. It is possible to correct for this assuming a particular model for the motion of the molecule, although very few crystallographers actually do so in practice!
Computer Calculation
In practice all bond lengths and angles are calculated routinely
(or at least they should be) by the
computer as part of the crystal structure refinement procedure.
In addition to needing information as supplied in the table on sulphur
hexafluoride, many programs will also need additional information.
Thus, there may be the option of limiting the calculation of
distances to be within a certain range. For a given atom, the computer
program will loop through the calculation of r using the
coordinates of all atoms in the unit cell, i.e. it will use the
coordinates of atoms generated by symmetry as well as those listed
in the table. In addition, it will apply unit cell translations (i.e.
± 1.0) to
each of the fractional difference values,
Δx, Δy, and Δz.
The importance of this is quickly demonstrated. If one atom is near the edge
of a unit cell, then the fractional difference value might be −0.73,
but a much smaller fractional difference will be 0.27
(
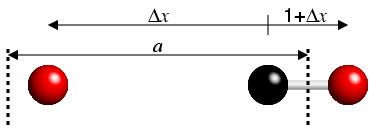
| © Copyright 1997-2006. Birkbeck College, University of London. | Author(s): Jeremy Karl Cockcroft |