What is Powder Diffraction?

Course Material Index  Section Index  Previous Page  Next Page 

What is Powder Diffraction?

One of the temporary difficulties that most students experience at this point is that ideally they need to understand several concepts all simultaneously; that is powder diffraction, Bragg's Law, crystal planes and monochromatic diffraction are all needed. However we need to start somewhere, so we will tackle powder diffraction first and catch up with the others afterwards.

To get going, we need to simplify down by considering an individual case which we can do with the aid of the illustration below. Let us imagine that X-rays of a given wavelength are incident on just one crystallite within a powder. It won't necessarily produce diffraction (diagram 1); in fact Laue's explanation and Bragg's Law (which as we have said comes later) show that the crystallite must be correctly oriented with respect to the X-ray beam in order for it to diffract. Here it helps if one imagines that the crystal is composed of many sets of planes that extend completely through the crystal (more about planes also later). Imagine one such set of planes (purple) in diagram 1. If we were to rotate the crystallite the planes would rotate with the crystal and there would come a point, diagram 2, when these planes are correctly oriented with respect to the X-ray beam to diffract (Bragg's law, later, shows this), the atoms scattering in phase and producing an intense diffracted ray.

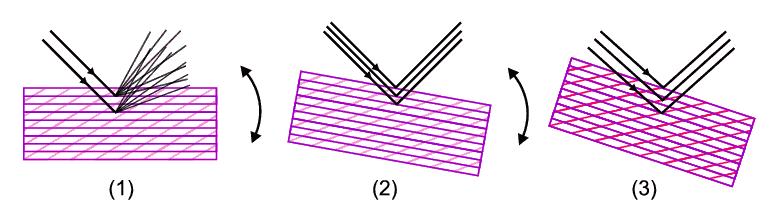
If we continue rotating, there would come another point, diagram 3, when a different "second" set of planes (in red) also comes into an orientation able to promote diffraction. Extending this argument, if we eventually reorient the crystallite through all possible orientations then every conceivable plane will at some point have had an opportunity to diffract (when it was correctly oriented with respect to the incident X-ray beam) and, over time, we would produce many diffracted rays. And here is the beauty of powder diffraction: we do this in powder diffraction, but not directly by re-orienting a single crystallite, but rather we do it statistically. By this we mean that a proper powder consists of many millions of crystallites, each at different orientations and so in presenting a powder to an X-ray beam, every possible orientation of a given set of planes will be shown to the X-ray beam. Statistically speaking some are bound to be at the correct orientation for diffraction to occur. Extending the argument, any other "second" set of planes will similarly be multiply represented and statistically there will be other crystallites that will be correctly oriented to promote diffraction from a second set of planes. The schematic below illustrates this idea in which, of all the crystallites present, two as it happens (the red pair) are oriented so as to diffract from one set of planes and another two (the green pair) are oriented so as to diffract from a different set of planes.

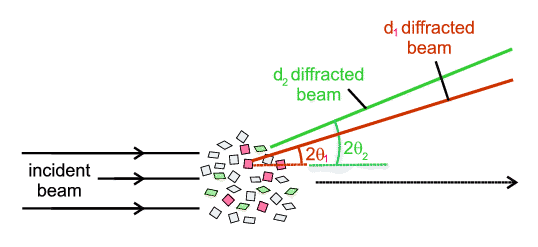
Extending this argument indefinitely, all planes that can diffract will "get their chance" with a powder. The beauty then of powder diffraction is that without necessarily any mechanical rotation one can promote diffraction from all potential planes. In saying this we have made some assumptions about the quality of the powder, but that is another story.

Course Material Index  Section Index  Previous Page  Next Page