 |
A little more on Crystal Planes |
 |
A little more on Crystal Planes |
A little more on Crystal Planes
Crystal planes is an important concept used in powder diffraction and crystallography in general. One can imagine a crystal being sub-divided into smaller component units; crystallographers use, depending on context, two alternative sub-divisions: one is the unit cell, the crystal building block, which we will return to later, and the other components are sets of planes invariably known as diffracting planes, reflecting planes, Bragg planes, crystal planes or hkl planes. A set of such planes consists of parallel evenly spaced planes which are extended to exactly fill the entire crystal; each plane is an equal distance, d (the inter-planar spacing), from its neighbouring plane. There are however an infinite number of such types of planes that can be devised and, between them all, they cover every region of space, and indeed every atom, within the crystal: this is one of the properties that makes their concept useful.
It is necessary to have some method of identifying and visualising the most useful planes. Crystallographers use an identification system referred to as Miller, or hkl, indices ( a sort of zip-code for the planes). Miller indices are simply a set of three numbers, hkl, which can take on any combination of three integer values between +∞ and −∞, e.g. (111), (-501) and (7-2-2). Each combination of hkl describes a unique set of planes filling the crystal and so hkl is often presented as a subscript to a property: e.g. dhkl which therefore means the d spacing between the planes defined by hkl. The Miller indices, hkl, also provide a useful means for visualising the planes. The convention is that if you have three axis, x,y,z, with three unit spacings, a,b,c, on each then one of these hkl planes can be visualised as the plane which intersects the x,y,z-axes at distances of a/h, b/k, c/l respectively. The next such plane parallel to this would pass through the origin. The illustration below shows an example of such a set of planes for the case of hkl = (222).
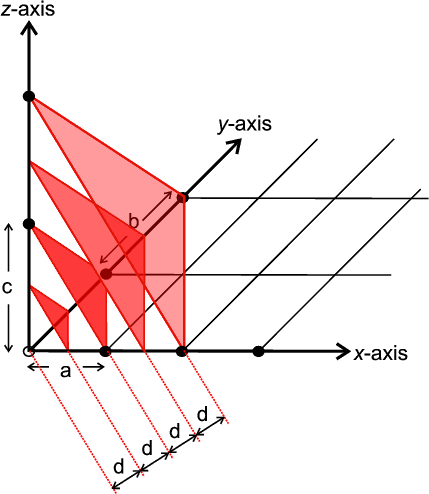
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Paul Barnes Tony Csoka Simon Jacques |