 |
Determination of Size and Strain |
 |
Determination of Size and Strain |
Determination of Size and Strain
The previous section explained how size and inhomogeneous strain can broaden the powder diffraction peak. A question that has occupied the minds of many powder diffractionists during the last (20th) century is whether the mean size and strain within a powder can be calculated from the diffraction pattern even when both are present simultaneously. We answer this question in both an approximate and more rigorous fashion.
Williamson-Hall Plot
This method is attributed to G.K.Williamson and his student, W.H.Hall (Acta Metall. 1, 22-31 (1953)). It relies on the principle that the approximate formulae for size broadening, βL, and strain broadening, βe , vary quite differently with respect to Bragg angle, θ:
| βL = | Kλ |
| βe = | Cε tanθ |
One contribution varies as 1/cosθ and the other as tanθ. If both contributions are present then their combined effect should be determined by convolution. The simplification of Williamson and Hall is to assume the convolution is either a simple sum or sum of squares (see previous discussion on Sources of Peak Broadening within this section). Using the former of these then we get:
| Kλ |
If we multiply this equation by cosθ we get:
| βtot cosθ = Cε sinθ + | Kλ L |
and comparing this to the standard equation for a straight line (m = slope; c = intercept)
we see that by plotting βtotcosθ versus sinθ we obtain the strain component from the slope (Cε) and the size component from the intercept (Kλ/L). Such a plot is known as a Williamson-Hall plot and is illustrated schematically below (note that this plot could alternatively be expressed in reciprocal space parameters, β* versus d*):
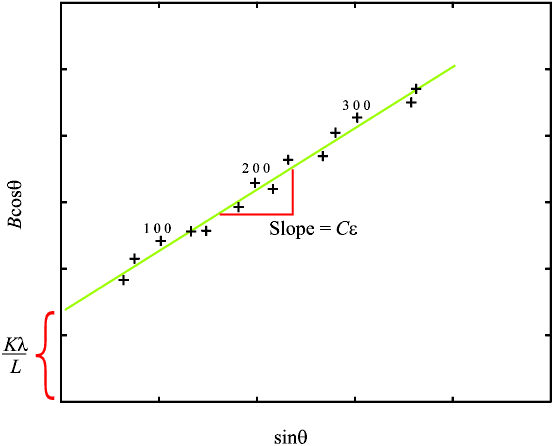
It can be a good idea to label each data point on the Williamson-Hall plot according to the index of its reflection to see whether any pattern emerges: for example, in the illustration several h00 reflections seem to lie slightly above the mean straight line suggesting that the powder crystallites are thinnest in the <100> crystal direction. However the Williamson-Hall method has many assumptions: its absolute values should not be taken too seriously but it can be a useful method if used in the relative sense; for example a study of many powder patterns of the same chemical compound, but synthesised under different conditions, might reveal trends in the crystallite size/strain which in turn can be related to the properties of the product.
Warren-Averbach method
This method is attributed to B.E.Warren and B.L.Averbach (J.Appl.Phys. 21, 595(1950) and ibid 23, 497 (1952)) and has become accepted as one of the more rigorous and widely used methods for separating the effects of size and strain. The treatment behind the method is quite complex and involves expressing the peak intensity in terms of a Fourier sum, which has distinct mathematical advantages (half of the terms - the sine components - turn out to be negligible, and (de-)convolution is conveniently handled in Fourier space). A further trick used is to arrange the powder diffraction peaks of a given pattern into h,k,l-indexed groups possessing a common crystallographic direction (e.g. <00n> = <001>, <002>, <003> where n is referred to as the order). This has two particular advantages: it overcomes the problem of asymmetrically sized/strained crystallites as each group analysis then becomes specific for a given direction (i.e. <001> in the above example), and the size/strain separation is simplified by the fact that the size effects are independent of order, n, whereas the strain effects vary with order. The method is exact if the strain distribution in the crystallites are Gaussian, and is still a good approximation otherwise provided the crystallite lattice distortions are small. The kind of final values provided by the method are an average (area-weighted) crystallite size, a parameter that is related to the crystallite size distribution and an average strain (for a characteristic size), all specified for a particular crystallographic direction. Even though the method is clearly not straightforward most commercial powder diffractometer systems provide a Warren-Averbach analysis routine on their software with easy-to-follow instructions.
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Paul Barnes Simon Jacques Martin Vickers |