Peak Shape Functions: Gaussian

Peak Shape Functions

I. Gaussian

Course Material Index

Section Index

Gaussian

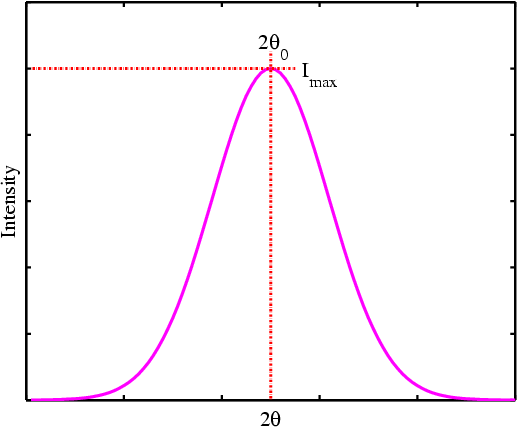
The Gaussian function is possibly the best-known peak function in the whole of science since many physical and chemical processes are governed by Gaussian statistics. Translated into powder diffraction terms, the function for the intensity at any value of 2θ near the peak becomes:

I(2θ) = I_max exp [ − π (2θ − 2θ₀)² / β² ]

where I_max is the peak intensity, 2θ₀ is the 2θ position of the peak maximum, and the integral breadth, β, is related to the FWHM peak width, H, by β = 0.5 H (π / log_e2)^1/2. The most important features of the Gaussian function are:

that it is easy to calculate
it is a familiar and well-understood function
it is a good function to describe both neutron and energy-dispersive X-ray powder diffraction peaks (it is however not good at describing angle-dispersive X-ray diffraction peaks)
it has a convenient convolution property (see later)
it is symmetrical

Because the intensity of a peak is essentially the peak area, it is often convenient to normalise the above Gaussian function so the peak area is unity; i.e.

G = √ (4 log_e2 / π) (1 / H) exp {− 4 log_e2 (2θ − 2θ₀ )² / H² }

An equation of this form is often applied in Rietveld programs and will be used later in the course.

Course Material Index

Section Index

Author(s): Paul Barnes
Simon Jacques
Martin Vickers