 |
Mode (5): Energy-dispersive |
Course Material Index
Section Index
Previous Page
Next Page
Mode (5): Energy-dispersive
The energy-dispersive diffraction (EDD) method is an alternative to line/area
detectors for reducing loss of useful diffraction information. The basic idea
behind position sensitive detectors was to recoup the diffraction information
lost through being spread out over the whole 2θ angular range; the
corresponding recoup with EDD is to use the full range of X-ray photons
emerging from the synchrotron rather than the small proportion passed by a
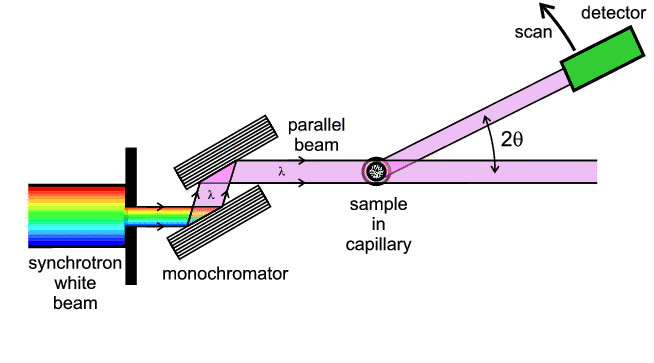
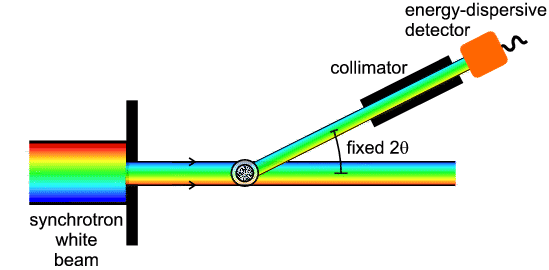
monochromator. The relationship between EDD and conventional diffraction can be
summarised by the following diagram:
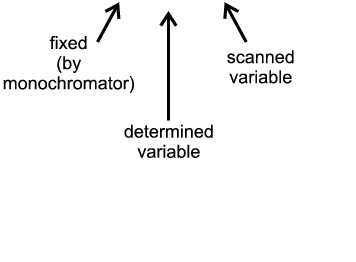
| Angle-Scanning |
|
|
λ = 2d sinθ
|
|
| Energy-Dispersive |
|
|
λ = 2d sinθ
|
|
This diagram shows that EDD and angular scanning diffraction are just two
different ways of treating the same principal variables (λ, d and
θ) in Bragg's Law. There are of course notable differences in the actual
experimentation involved. By contrast with angle scanning diffraction, with EDD
the whole available X-ray wavelength/energy spectrum is usually incident on the
sample, and the process of diffraction in effect then selects out which
wavelength/energy is diffracted in a given direction 2θ. The post-sample
collimator defines the angle 2θ and the detector not only has to be able
to detect X-ray photons but also measure their energy. Energy relates to
wavelength by the frequency ν, Plank's constant, h, and the speed of
light, c:
E = hν = hc / λ
Rewriting Bragg's law in terms of photon energy gives the energy-dispersive
form:
E d sinθ = C
where C is the EDD constant which has the value 6.1993 keVÅ.
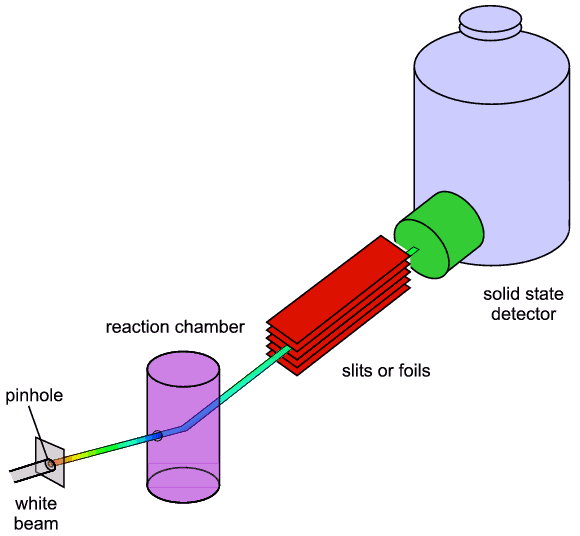
The detector is termed an energy-dispersive
detector and it is a key component in the whole set-up. A schematic of a basic
energy-dispersive diffractometer is shown below:
The main advantages of EDD are:
-
there are in principle no moving parts with an EDD, which leads to the 2
following advantages:
-
dynamic data collection is simple and extremely rapid (e.g. 1 second
diffraction patterns are not uncommon);
-
since there is no angular scanning involved the X-ray entrance/exit
windows can be small and therefore it is much easier to design sample
environmental heating/cooling cells;
-
the white energetic X-ray beam emerging from a synchrotron (e.g.
20-150 keV) is very penetrating so that truly bulk samples can be analysed
(typically samples are 5-25 mm thick even with such materials as
alumino-silicates).
The main disadvantages of EDD are:
-
the quality of the diffraction pattern is intrinsically limited by the
performance of the ED-detector and currently this means that the diffraction
peaks are much broader than in the equivalent angle-scanning patterns;
-
a consequence of the above is that if diffraction peaks are close
together they are likely to overlap in EDD data. This and other
factors (X-ray absorption, the intensity-energy spectrum of the synchrotron
source) make it very difficult to perform structure refinement from
EDD-data.
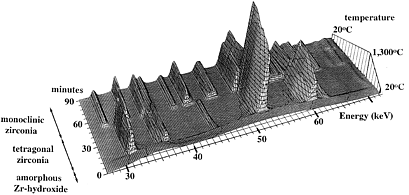
Despite its limitations, EDD is an extremely versatile technique for studying
rapid transformations and reactions in solid state science. A dramatic example
of this power is illustrated in the data plot below which shows an amorphous
zirconium hydroxide crystallising to monoclinic zirconia on being heated to
1300°C, and then transforming to tetragonal zirconia on cooling back to
room temperature.
Click image to enlarge.
Course Material Index
Section Index
Previous Page
Next Page