 |
Calculating the Intensity of Diffraction Using the Structure Factor Equation |
 |
Calculating the Intensity of Diffraction Using the Structure Factor Equation |
Calculating the Intensity of Diffraction Using the Structure Factor Equation
This is a very important sub-section. Whatever you may or may not have understood during the theory and explanations of these last two sections, it is vital that you do at least learn how to calculate predicted intensities from a known structure. So this sub-section will take you step by step through this procedure.
Even though the calculation starts with a formula containing a complex number, this is really just a piece of convenient notation. Very quickly the calculation boils down to little more than adding up values of sines and cosines of angles. The calculation is procedural; here we will go through one part, in more detail than one would ordinarily, and ask you to calculate some others in an assignment. The calculations enable one to solve the following problem:
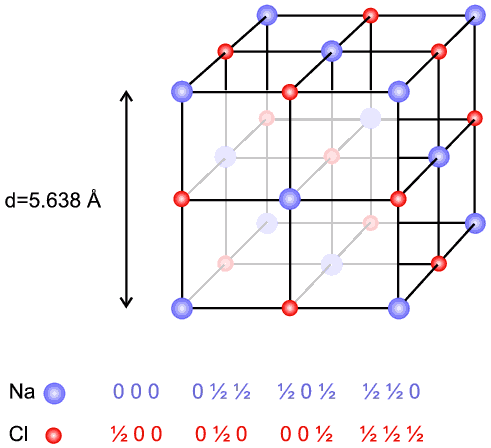
Sodium chloride (NaCl) is a face centred cubic structure (below figure) with a unit cell d spacing of 5.638 Å and fractional coordinates for the 4 Na and 4 Cl ions as follows:
| Na: | 0, 0, 0; | 0, 1/2, 1/2; | 1/2 , 0, 1/2; | 1/2, 1/2, 0. |
| Cl: | 1/2, 0, 0; | 0, 1/2, 0; | 0, 0, 1/2; | 1/2, 1/2, 1/2. |
What are the relative intensities of the following reflections: 111, 200, 100? (This will involve calculating the ratio of, for example, the first two, i.e. I111 / I200 .)
We start with the fundamental structure factor equation:
| F(S) = | Σ n |
fn e2π i (hx + ky + lz) |
An explanation en route:
This complex form is used to represent the fact that the diffracted wave has an amplitude and a phase. The equation is really a notational way of saying there are two parts: a sine part and a cosine part,
| F(S) = | Σ n |
fn cos {2π (hx + ky + lz)} + i | Σ n |
fn sin {2π (hx + ky + lz)} (in radians) |
| F(S) = | Σ n |
fn cos {360 (hx + ky + lz)} + i | Σ n |
fn sin {360 (hx + ky + lz)} (in degrees), |
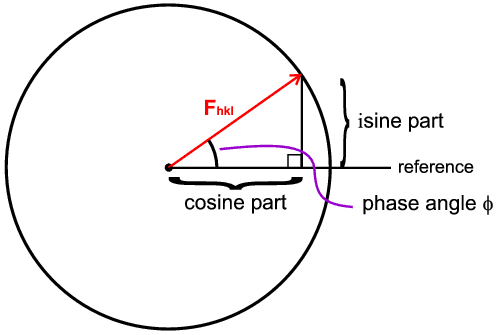
The amplitude is represented as the radius of the circle and the phase as the angle made to a reference direction (horizontal). In general we calculate the cosine and sine parts separately and then combine them using Pythagoras' theorem to get the final amplitude.
Returning to the calculation of the 111 intensity; the rest of the calculation procedure is sub-divided for help and reference:
(1) Using Crystallography and Bragg's law
We need to calculate the d spacing of the reflection involved. The formula for d for cubic crystals is:
| dhkl = a / √(h2 + k2 + l2 ) |
| d111 = 5.638 / √(12 + 12 + 12 ) = 5.638 / √3 = 3.255 Å |
| λ = 2d sinθ |
| sinθ / λ = 1 / 2d = 1 / (2 × 3.255) = 0.154 Å−1 |
(2) Working out what atomic scattering factors (fn) we will need
The atomic scattering factors for Na+ and Cl− ions can be obtained from the International Crystallographic Tables. They vary with sinθ / λ for reasons that were explained earlier (the "atomic form factor"). We have calculated above that for the 111 reflection, sinθ / λ = 0.154 Å−1. If we consult the International Crystallographic Tables we get the following f values (in numbers of electrons) in the range 0.0 to 0.2:
| sinθ / λ | 0.00 | 0.05 | 0.10 | 0.15 | 0.20 |
| fNa+ | 10.0 | 9.884 | 9.551 | 9.035 | 8.39 |
| fCl− | 18.0 | 17.46 | 16.02 | 14.12 | 12.20 |
We could approximate to the values for 0.15 (since 0.154 is much closer to 0.15 than 0.20) or be a little more accurate and use an intermediate value weighted more heavily towards the 0.15 value (by 0.046:0.004). This produces the following result (needed values in bold):
| sinθ / λ | 0.15 | 0.154 | 0.20 |
| fNa+ | 9.035 | 8.98 | 8.39 |
| fCl− | 14.12 | 13.97 | 12.20 |
(3) Working out the cosine part of F111
We will perform this part in degrees and the next in radians, so that you can see how to calculate the values by either convention. The cosine part for F has 8 terms corresponding to the 8 atoms involved. Inserting the appropriate f values, coordinates and hkl = 111 gives:
|
Σ n |
fn cos{360 (hx + ky + lz)} | = | 8.98 cos {360 (1 × 0 + 1 × 0 + 1 × 0)} | |
| + | 8.98 cos {360 (1 × 0 + 1 × 1/2 + 1 × 1/2)} | |||
| + | 8.98 cos {360 (1 × 1/2 + 1 × 0 + 1 × 1/2)} | |||
| + | 8.98 cos {360 (1 × 1/2 + 1 × 1/2 + 1 × 0)} | |||
| + | 13.97 cos {360 (1 × 1/2 + 1 × 0 + 1 × 0)} | |||
| + | 13.97 cos {360 (1 × 0 + 1 × 1/2 + 1 × 0)} | |||
| + | 13.97 cos {360 (1 × 0 + 1 × 0 + 1 × 1/2)} | |||
| + | 13.97 cos {360 (1 × 1/2 + 1 × 1/2 + 1 × 1/2)} | |||
| = | 8.98 cos 0 + 8.98 cos 360 + 8.98 cos 360 + 8.98 cos 360 | |||
| + | 13.97 cos 180 + 13.97 cos 180 + 13.97 cos 180 + 13.97 cos 540 | |||
| = | 8.98 + 8.98 + 8.98 + 8.98 − 13.97 − 13.97 − 13.97 − 13.97 | |||
| = | − | 19.96 |
(4) Working out the sine part of F111
We will perform this part in radians. Again inserting the appropriate values gives:
|
Σ n |
fn sin {2π (hx + ky+ lz)} | = | 8.98 sin {2π (1 × 0 + 1 × 0 + 1 × 0)} | |
| + | 8.98 sin {2π (1 × 0 + 1 × 1/2 + 1 × 1/2)} | |||
| + | 8.98 sin {2π (1 × 1/2 + 1 × 0 + 1 × 1/2)} | |||
| + | 8.98 sin {2π (1 × 1/2 + 1 × 1/2 + 1 × 0)} | |||
| + | 13.98 sin {2π (1 × 1/2 + 1 × 0 + 1 × 0)} | |||
| + | 13.97 sin {2π (1 × 0 + 1 × 1/2 + 1 × 0)} | |||
| + | 13.97 sin {2π(1 × 0 + 1 × 0 + 1 × 1/2)} | |||
| + | 13.97 sin {2π (1 × 1/2 + 1 × 1/2 + 1 × 1/2)} | |||
| = | 8.98 sin 0 + 8.98 sin 2π + 8.98 sin 2π + 8.98 sin 2π | |||
| + | 13.97 sin π + 13.97 sin π + 13.97 sin π + 13.97 sin 3π | |||
| = | 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 | |||
| = | 0 |
(5) Combining the cosine and sine parts of F111
Mathematically we would present this as a complex number result:
| F111 = −19.96 + i × 0 |
so
| Fhkl2 | = | {cosine part}2 + {sine part}2 |
| Fhkl2 | = | (− 19.96)2 + 02 = 398 |
(6) The intensity I111
Since the diffraction experiment measures the squares of the amplitudes (but not phase information) assuming we have kinematic diffraction, then a very crude value for the peak intensity, which makes no allowance for any correction factors, might simply be given as:
| I111 = F1112 = 398 units |
One might ask what the units are in this answer. As the key parameters (f, atomic scattering factors) are defined as being relative to a single electron, we simply say that the amplitude of the 111 reflection from NaCl is 19.96 times stronger than we would get from a single electron and the intensity of the 111 reflection is 398 times what we would get from a single electron. If one recalls that 4 units of NaCl possess a total of 112 electrons (which squared is 12544) you get some idea of the fall off in amplitude (112 to 19.96) and intensity (12544 to 398) due to the combined effects of the atomic scattering "form" factor and interference. You should be aware that the value of 398 is for one unit cell of NaCl.
(7) The intensities I200 and I100
You may like to try these out for yourselves. You will see the answer later for the calculation of the structure factor of the 200 reflection. You should find that the answer for I100 is zero. You will learn more about the reasons for this later in the course. However, our next step is to discuss how "true" relative intensities are calculated.
|
© Copyright 1997-2006.
Birkbeck College, University of London.
|
Author(s):
Paul Barnes Simon Jacques Martin Vickers |