Kinematic versus Dynamic Diffraction

Course Material Index  Section Index  Next Page

Kinematic versus Dynamic Diffraction

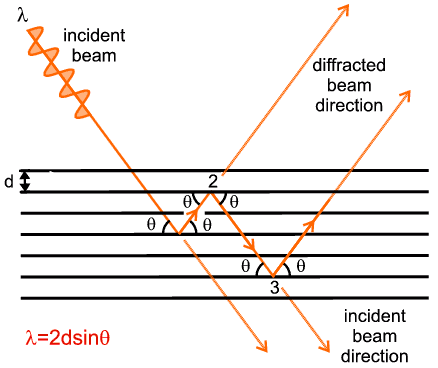
The theory has been developed so far on the underlying assumption that each individual diffraction/interference event, from whatever locality within the crystal, acts independently of the others. Away from this simplicity there are many complications that can occur. To begin with one should note that if an X-ray beam is incident at an angle θ that satisfies Bragg's law, it will be reflected at the angle θ to these planes (as shown below). It follows then that the diffracted ray will continue to satisfy Bragg's law and therefore is at the correct Bragg angle to diffract a second time (location 2 in the diagram) so that it then travels in the direction of the original incident beam; similarly it remains available for diffraction a third time (location 3), back into the first diffraction direction, and so on.

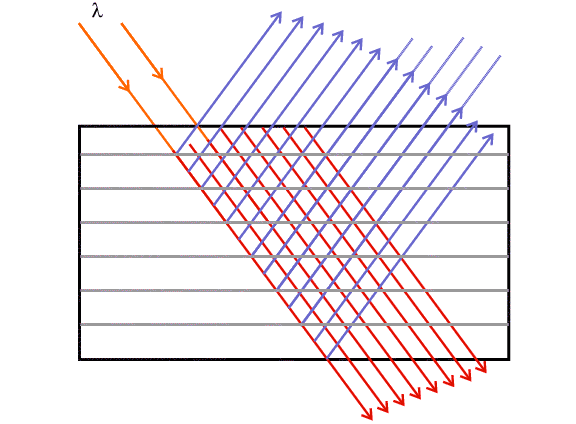
Suppose that the whole crystal is perfect and is bathed with X-rays which are subject to multiple diffraction throughout the crystal; all of these waves can then intefer with each other. This process was described by Ewald during the early part of the 20th century. Its theory, in which the diffraction intensity, I, is proportional to just the magnitude of the structure factor, F, is referred to as the dynamical theory of diffraction. Dynamic diffraction is illustrated very schematically in the diagram below and may be observed in large near-perfect single crystals, such as those grown for the semi-conductor industry.

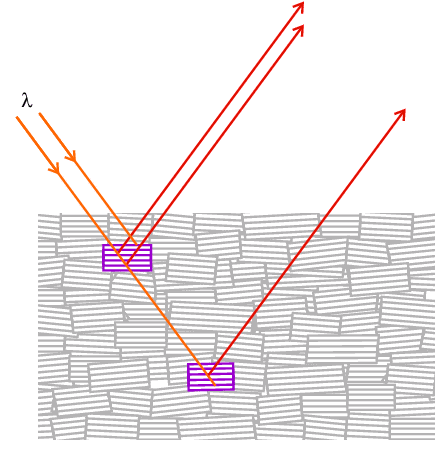
In practice, dynamic effects are relatively rare because most crystals are not perfect but consist of slightly mis-oriented "mosaic" blocks as in the final diagram below. Therefore when an imperfect crystal is subjected to an X-ray beam only a small fraction of the mosaic blocks will be exactly at the Bragg condition and capable of diffracting (two such blocks in the case of the illustration below). As the crystal is rotated slightly, some mosaic blocks will move away from the Bragg condition while others will move towards it. So during a complete angular scan, the full diffracting power of the crystal will still be measurable, but obviously the mosaic spread will lead to a broadening of the diffraction peaks. The mosaic blocks in effect break up the links between the different parts of the diffracting crystal so that the multiple interference effects of the dynamic case do not occur. The kinematic theory of diffraction, which states that the intensity is proportional to the square of the structure factor, then holds approximately. Kinematic diffraction is the norm in crystallography; you might live a crystallographic life without ever coming into contact with dynamic effects; but just in case you do, you have been warned that it is possible to have crystals "too perfect" for your own good!

Course Material Index  Section Index  Next Page